代数几何简介

1. Introduction

代数几何是数学的核心领域，也是如今国际数学界的主流。代数几何与许多数学分支都存在广泛的联系，比如数论、微分几何、代数拓扑、复几何、表示论、同调代数、交换代数、偏微分方程等等，这些分支的发展同时也对代数几何起到促进作用。数学史上的许多重大的事件，比如，费马大定理、莫德尔猜想、韦伊猜想的证明都跟代数几何有关。同时，代数几何存在广泛的应用，比如密码学、弦理论、大数据、统计学习理论等等。代数几何之下有众多分支，比如复代数几何，热带几何，算术几何，远阿贝尔几何，$p$进霍奇理论（complex algebraic geometry, tropical geometry, arithmetic geometry, anabelian geometry, p-adic hodge theory），每个分支代表代数几何研究的一个大方向，而在每个大方向下，又有各种以不同的问题为导向的子方向。在这篇文章中，我们将会对代数几何，包括它的分支算术代数几何，做一个简短的介绍。

2. An Introduction to Arithmetic Geometry

算术几何是算术代数几何的简称，它是代数几何的一个分支，主要研究与数论有关的问题，比如丢番图方程。著名的费马大定理其实就是丢番图方程的一种。

Definition 2.1. Diophantine equations are equations whose solutions are required to be integers.

Example 2.2. The equations in Fermat's Last Theorem : $x^{n} + y^{n} = z^{n}$ for all integers $n\geq 2$ are Diophantine equations.

Example 2.3. The equations $ax + by = c$ are called linear Diophantine equations.

Example 2.4. The equations $x^{2} + y^{2} = z^{2}$ are called Pythagorean equations.

从上可以看出椭圆曲线与丢番图方程之间存在某种联系，因此数论上的问题就可以转移到几何上的椭圆曲线进行研究。接下来，我们将给出椭圆曲线的定义，但是在此之前我们先做一些约定。我们记$K$为一个任意的域，$f(x)\in K[x]$ 为$K$上的一个三次多项式，假设这个多项式有不同的根，由于这个域并不一定是代数闭域，因此有些不同的根存在于这个域的代数闭包 $\overline{K}$上。同时，我们假设域$K$不是特征2的。

Definition 2.5. The solutions to the equation $y^{2} = f(x)$ , where $x$ and $y$ are in some extension $K'$ of $K$, are called the $K'$-points of the elliptic curve defined by the equation.

Example 2.6. The locus of the equations $y^{2} = x^{3} - n^{2}x$ is a special case of elliptic curve.

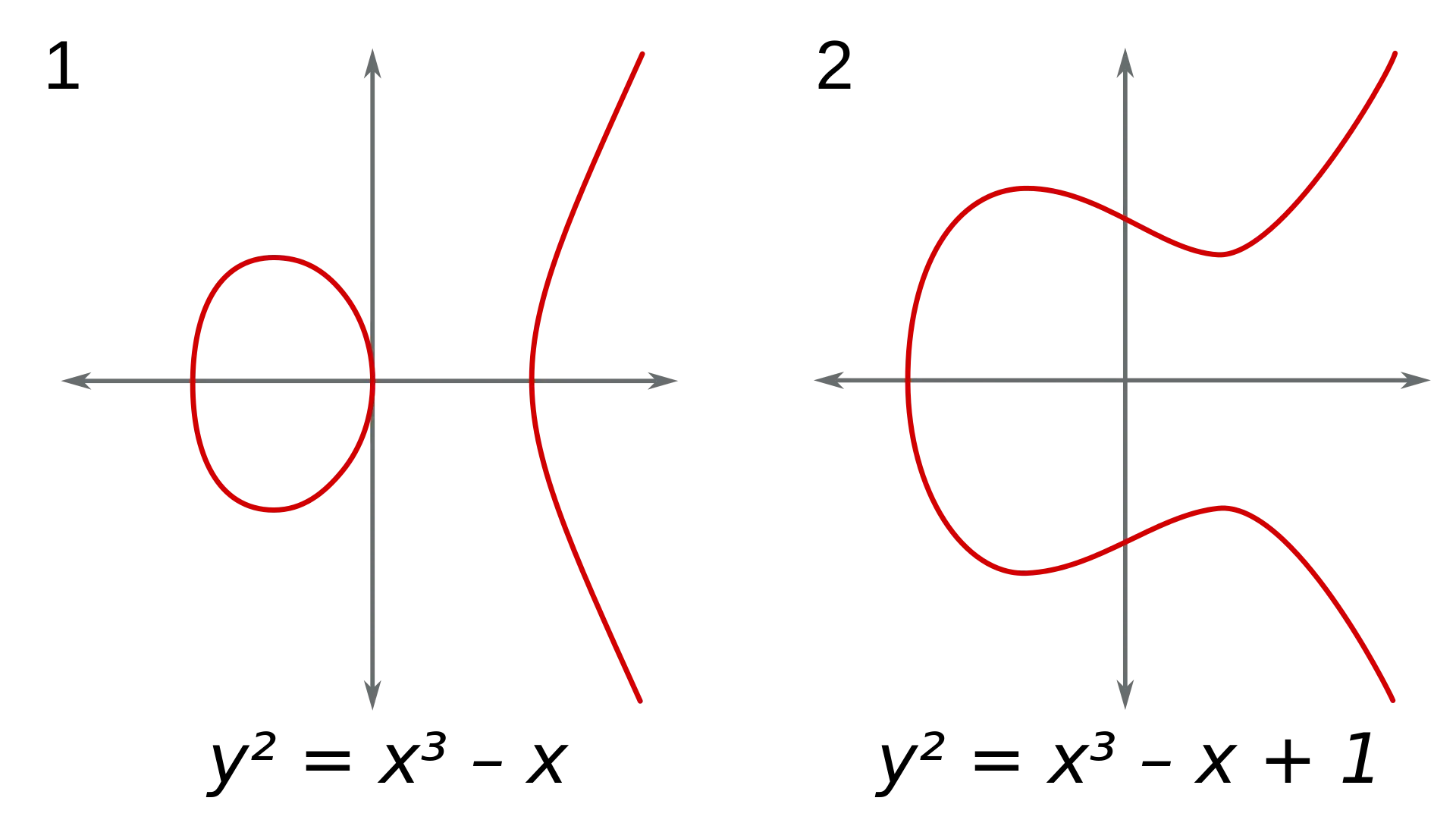
Figure 1. Elliptic curves

从上面的定义和这个例子，我们可以看出椭圆曲线的方程形式上像一个丢番图方程。事实上，当我们限定椭圆曲线方程的解为整数解时，方程就成为了丢番图方程。

既然说到了椭圆曲线，我们不得不提及一下跟椭圆曲线有关联的椭圆函数。椭圆函数是19 世纪数学最光辉的成就之一，它当初是由求椭圆弧长诱导出来的，与椭圆积分也有很密切的联系，毕竟椭圆积分就是用来求椭圆弧长的。顺带一提，椭圆周长目前没有办法求精确值，其周长表达式没法表达成初等函数的形式，它只有椭圆积分表达式以及级数展开式。在定义椭圆函数之前，我们需要先定义复数域$\mathbb{C}$上的lattice。

Definition 2.7. A lattice $L$ in the complex plane is the set of all integral linear combinations of two given complex numbers $\omega_{1}$ and $\omega_{2}$, where $\omega_{1}$ and $\omega_{2}$ are linear independent.

Example 2.8. If we take $\omega_{1}$ = 1 and $\omega_{2}$ = $i$, we will get a lattice of Gaussian integers $\{mi+n| m , n\in \mathbb{Z}\}$.

Definition 2.9. A meromorphic function on $\mathbb{C}$ is said to be an elliptic function relative to a given lattice $L$, if $f(z+l)=f(z)$ for all $l\in L$.

从定义可以看出，椭圆函数是一个双周期的函数。这使人联想到实数情况的单周期函数。一个$\mathbb{R}$上的周期函数，可以看成一个圆上的函数，而一个$L$的椭圆函数则可以看成一个圆环上的函数。我们可以证得关于一个lattice 的所有椭圆函数的集合构成一个域$\mathcal{E}_{L}$，它是所有亚纯函数的域的子域，因为任意两个椭圆函数的和差积商都是椭圆函数。

接下来，我们继续讨论椭圆曲线。椭圆曲线与模形式有紧密的关联，而它们之间的联系成为了证明费马大定理的关键。由于作者并不能完全看懂费马大定理的证明，因此这里不做过多阐述。我们知道当年最后完成费马大定理证明的数学家是Wiles，而Wiles在他的paper 中证明了所有有理数集上的半稳定的椭圆曲线都是modular的，从而使费马大定理成为一个推论被证明。值得一提的是，Wiles在十岁的时候在一本叫做《最后定理》的书中了解到了费马大定理，他很受震撼并打算成为第一个解决费马大定理的人，最后正如他自己所说，很多数学家用自己的一生尝试解决费马大定理都没有成功，最后只有他成功了。关于椭圆曲线、椭圆函数、模形式、费马大定理的证明，想了解更多的读者可以参考[1], [11]。

讲完费马大定理，接下来我们来讲讲费马大定理背后的故事，即费马大定理之所以最后能够被Wiles证明，主要是归功于某些数学家的关键性工作。其中两位即是日本数学家Shimura 和Taniyama，他们提出的谷山—志村猜想成为了证明费马大定理的关键一步。还有一位数学大师，在讲他之前我们需要先做一些铺垫。上个世纪，算术几何中不仅仅只有费马大定理，还有韦伊猜想（有限域上的黎曼猜想）、莫德尔猜想。韦伊猜想被Deligne所证明，而莫德尔猜想被Faltings所证明。Deligne和Faltings都是如今数学界的泰斗级人物，不论是Wiles、Deligne还是Faltings ，他们的证明都离不开一个人的奠基性工作，他就是被很多人认为是20世纪最伟大的数学家Grothendieck。Grothendieck被称作代数几何的教皇，有一句很经典的描述他的话就是：“20世纪代数几何涌现了很多天才和菲尔兹奖，但是上帝只有Grothendieck一个。”

Grothendieck的工作使代数几何这门古老的学科重新焕发出新的生命力，这也使代数几何进入如今的黄金时期。Grothendieck的哲学直接被数学所吸收，以至于现在数学的新人根本无法想象Grothendieck时代前这个领域的模样。从二十世纪中叶开始，整个代数几何领域越来越抽象和普遍的研究倾向，大部分都得归功于Grothendieck的影响。Grothendieck 的影响之大，几乎所有数学分支都能感受到。如今的代数几何已经是后Grothendieck时代了，代数几何涌现出了很多后起之秀，比如说日本数学家Shinichi Mochizuki、德国数学家Peter Scholze。

接下来，我们继续介绍算术几何的有关内容。上文中我们提到了可以通过研究椭圆曲线和模形式，进而研究数论问题。而椭圆曲线其实只是代数曲线中的一种特殊情况，代数曲线是算术几何的一个重要研究课题。别看名字很高大上，它其实很常见，比如说在欧几里得平面上的代数曲线，就是我们用多项式方程$f(x,y) = 0$所定义的平面曲线。而想要定义一般的代数曲线就不那么简单了，这需要用到Grothendieck发展的概形的理论。在定义一般的曲线之前，我们需要不少的预备知识，因此在这里我们只做简单的描述，想要了解更多细节的读者可以参考[2]。

首先，在定义概形之前，我们需要定义层的概念。我们有阿贝尔群层、环层、模层等等，取决于层所取的范畴。关于范畴论的概念不熟悉的读者可以参考[7]。

Definition 2.10 ([2], [16]). Let $X$ be a topological space. A presheaf $\mathcal{F}$ of abelian group on $X$ is a contravariant functor $$ \mathcal{F}:\textbf{Top}^{\textrm{opp}}\rightarrow \textbf{Ab}$$ from the category of open sets of $X$ to the category of abelian groups.

If $\mathcal{F}$ is a presheaf on $X$, the set $\mathcal{F}(U)$ consists of the sections of $\mathcal{F}$ over the open set $U$. If $s\in \mathcal{F}(U)$, we write $s|_{V}$ for an element of $\mathcal{F}(V)$ corresponding to $s$.

Definition 2.11. A presheaf $\mathcal{F}$ on a topological space $X$ is a sheaf, if it satisfies the following conditions:

1. (Uniqueness) if $U$ is an open set of $X$, and $\{V_{i}\}$ is an open covering of $U$, then for an element $s\in \mathcal{F}(U)$ such that $s|_{V_{i}}$ = 0 for all $i$, we have $s = 0$.
2. if $U$ is an open set of $X$, and $\{V_{i}\}$ is an open covering of $U$. If we have elements $s_{i}\in \mathcal{F}(V_{i})$ for each $i$, such that for each $i, j$, $s_{i}|_{V_{i} \cap V_{j}} = s_{j}|_{V_{i}\cap V_{j}}$, then there is an element $s \in \mathcal{F}(U)$ such that $s|_{V_{i}} = s_{i}$ for each $i$.

Definition 2.12. Let $\mathcal{F}$ be a presheaf on $X$, if $P$ is a point of $X$, we define the stalk $\mathcal{F}_{P}$ of $\mathcal{F}$ at $P$ to be direct limit of the groups $\mathcal{F}(U)$ $$\lim\limits_{\longrightarrow}\mathcal{F}(U)$$ for all open sets $U$ containing $P$.

一个预层上某个点的茎$\mathcal{F}_{P}$，其实就是一个等价类的集合，我们可以记茎中任意一个元素为$\langle U,s\rangle$，并称它为$\mathcal{F}$截面的芽。其中$U$为$P$ 点的开邻域，$s\in\mathcal{F}(U)$。

接下来，我们记$A$为一个环，$Spec(A)$为该环所有素理想的集合，称为谱。如果$\alpha$是环$A$的任意一个理想，我们记$V(\alpha)\subseteq Spec(A)$为所有包含理想$\alpha$ 的素理想的集合。我们令$V(\alpha)$为$Spec(A)$中的闭集，从而在$Spec(A)$上定义了一个Zariski拓扑。接着，我们再定义拓扑空间$Spec(A)$上的环层$\mathcal{O}$。 这样下来，$(Spec(A),\mathcal{O})$成为一个局部赋环空间。接下来我们给出赋环空间的定义。

回顾一下，一个环$A$被称为局部环，如果它只有唯一一个极大理想$\mathfrak{m}_{A}$。

Definition 2.13. A ringed space is a pair $(X,\mathcal{O}_{X})$, where $X$ is a topological space and $\mathcal{O}_{X}$ is a sheaf of rings on $X$ called the structure sheaf. A ringed space is a locally ringed space, if for each $P\in X$, the stalk $\mathcal{O}_{X,P}$ is a local ring.

有了上面这些储备，我们终于可以定义概形。首先我们定义仿射概形，之后就是一般的概形。

Definition 2.14. An affine scheme is a locally ringed space $(X,\mathcal{O}_{X})$, which is isomorphic to a spectrum $\textrm{Spec }A$ of some ring $A$. A scheme is a locally ringed space $(X,\mathcal{O}_{X})$ in which every point $p$ of $X$ has an open neighborhood $U$ such that $(U,\mathcal{O}_{X}|_{U})$ is an affine scheme.

从以上的定义，我们可以看出概形跟流形有异曲同工之妙。对于一个流形来说，它局部上都是一个欧几里得空间。而对于一个概形来说，它局部上都是一个仿射概形，同时因为同构关系，概形局部上的仿射概形可以看成某个环的谱。这样下来，流形由一个个欧几里得空间拼起来，而概形由一个个环的谱拼起来。而事实上，微分几何里的流形是可以用局部赋环空间表示的（更多细节请参考[10], [15]）。

现在我们有了概形，就可以定义一般意义上的代数曲线了。在此之前，我们先定义概形的一些基本性质。

Definition 2.15. Let $X$ be a scheme. We say that $X$ is integral if for each open affine set $U\subset X$, $\mathcal{O}_{X}(U)$ is an integral domain.

Definition 2.16. Let $f:X\rightarrow Y$ be a morphism of schemes. The diagonal morphism of $X$ is a morphism $\triangle:X\rightarrow X\times_{Y}X$ such that $\textrm{pr}_{1}\circ\triangle=\textrm{pr}_{2}\circ\triangle=\textrm{id}_{X}$. We say that $f$ is separated or that $X$ is separated over $Y$ if the diagonal morphism of $X$ is a closed immersion.

Definition 2.17. Let $f:X\rightarrow Y$ be a morphism of schemes. We say that $f$ is proper or that $X$ is proper over $Y$ if $f$ is separated, of finite type, and universally closed.

Definition 2.18. Let $X$ be a scheme. The dimension of $X$ is the dimension of its underlying topological space $\textrm{sp}(X)$, which we will denote by $\textrm{dim }X$.

Definition 2.19. An algebraic curve is an integral scheme of dimension 1, proper over a field $K$, all of whose local rings are regular.

因此，一个代数曲线其实就是一个一维的概形。流形也如此，一维的流形也叫做曲线。以上我们完成了对代数曲线的定义，通过代数曲线我们可以研究数论问题。但是，研究代数曲线是需要工具的。在这些工具中，就有algebraic stack和moduli theory。Algebraic stack是stack的特殊情况，stack是对概形的进一步推广。而stack可以看成某种群胚纤维化范畴(category fibred in groupoid)，可以运用Descent à la Grothendieck来定义。而moduli theory就是研究某一类数学对象的参数空间，比如曲线的模空间、椭圆曲线的模空间。由于目前这些理论不是作者的研究方向，作者不作过多阐述。

2.1 The $p$-adic numbers field $\mathbb{Q}_{p}$ and the $p$-adic integers ring $\mathbb{Z}_{p}$

接下来，我们来简单说明一下$p$进数域$\mathbb{Q}_{p}$是如何构造出来的。首先，我们以有理数域$\mathbb{Q}$为例，粗略解释一下完备化（completion）的过程：我们取有理数域所有柯西序列构成的集合，定义逐项加法和乘法后可以证明它构成一个交换环，接着模掉所有零序列构成的理想，我们就得到一个完备的域，它是有理数域的域扩张。一个域的完备化不是唯一的，对应不同定义于域上的绝对值，我们可以定义不同的柯西序列，进而构造出不同的完备化。在这里，我们给出任意域上的绝对值与完备域的定义。

Definition 2.20. Let $K$ be a field. An absolute value on $K$ is a map $\left|\cdot\right|:K\rightarrow\mathbb{R}_{\geq0}$ such that $\left|x\right|=0\Leftrightarrow x=0$, $\left|xy\right|=\left|x\right|\left|y\right|$, and $\left|x+y\right|\leq\left|x\right|+\left|y\right|$. We say that $K$ is complete if it is complete with respect to the distance $d(x,y)=\left|x-y\right|$ induced by the absolute value $\left|\cdot\right|$ on it.

接下来我们先定义有理数域上的$p$进序数。

Definition 2.21. Let $p$ be any prime number. We define the $p$-adic ordinal ord$_{p}a$ of an non-zero integer $a$ to be the highest power of $p$ which divides $a$, i.e. the greatest $m$ such that $p^{m}|a$ or $a\equiv0(\textrm{mod }p^{m})$.

我们约定当整数$a=0$时，ord$_{p}a=\infty$。接着对于任意$x=a/b\in\mathbb{Q}$，我们定义$\textrm{ord}_{p}x=\textrm{ord}_{p}a-\textrm{ord}_{p}b$。如果将ord看成一个函数，那么它是良定义的，因为如果将$x$写成$x=ac/bc$，我们有$\textrm{ord}_{p}x=\textrm{ord}_{p}ac-\textrm{ord}_{p}bc=\textrm{ord}_{p}a-\textrm{ord}_{p}b$。

接着我们定义$p$进绝对值：

$$\left| x \right|_{p} = \begin{cases} \frac{1}{p^{\textrm{ord}_{p}x}}, & \textrm{if} \ x\neq 0\\ 0,  & \textrm{if} \ x = 0. \end{cases}$$

我们先阐述复数域$\mathbb{C}$的构造过程，首先我们作有理数域$\mathbb{Q}$的完备化（关于通常的绝对值$\left|\cdot\right|$）$\widehat{\mathbb{Q}}$得到实数域$\mathbb{R}$，然后取实数域的代数闭包$\overline{\mathbb{R}}$ 得到复数域。$p$进数域$\mathbb{Q}_{p}$其实就是有理数域$\mathbb{Q}$的$p$进完备化（关于$p$进绝对值 $\left|\cdot\right|_{p}$）$\widehat{\mathbb{Q}}$。然而当我们取$p$进数域的代数闭包$\overline{\mathbb{Q}}_{p}$时，发现它不是完备的，因此我们对其再作一次完备化，最后得到$\mathbb{C}_{p}$。它是最小的包含有理数域的既是代数闭的，又是完备的域。

于是，我们有如下关系：

$$\begin{cases} \mathbb{C}_{p}=\widehat{\overline{\mathbb{Q}}}_{p}=\widehat{\overline{\widehat{\mathbb{Q}}}}, \textrm{p-adic analog} \\ \mathbb{C}=\overline{\mathbb{R}}=\overline{\widehat{\mathbb{Q}}}, \textrm{usual case} \end{cases}$$

接着$p$进整数环$\mathbb{Z}_{p}$即是$p$进数域$\mathbb{Q}_{p}$的离散赋值环：

$$\mathbb{Z}_{p}:=\{x\in\mathbb{Q}_{p}\mid \left|x\right|_{p}\leq1\}.$$

3. Grothendieck's Theory

接下来，我们来回顾一下上世纪Grothendieck所做的工作。其实代数几何如今整体上能分成两个方向，一个是以Grothendieck发展的抽象理论为基础的方向，另一个是与微分几何结合主要研究复几何的方向（参考[14]）。Grothendieck所做的工作当然远远不止上文所说的概形，还有étale cohomology（平展上同调）, crystalline cohomology（晶体上同调）, $l$-adic cohomology（$l$进上同调）, topos（拓扑范）, motives, Grothendieck topology, Grothendieck universe等等。

除此之外，Grothendieck 还有三本被誉为代数几何圣经的著作，分别是EGA(Éléments de géométrie algébrique),SGA(Séminaire de géométrie algébrique)和FGA(Fondements de la Géometrie Algébrique)，翻译成中文就是《代数几何原理》、《代数几何讨论班》和《代数几何基础》。

首先我们来说说Grothendieck著名的motives理论，该理论的哲学即是将所有的性质相似的上同调，诸如奇异上同调、德拉姆上同调、平展上同调和晶体上同调，统一起来。下面我们给出上同调的定义，该定义涉及到阿贝尔范畴。所谓的阿贝尔范畴，它的原型是阿贝尔群范畴，上世纪Grothendieck将其重要的性质抽象出来，只剩下足够计算同调代数的东西。

Definition 3.1. A cochain complex $\mathcal{C}= \{\mathcal{C}^{n},d^{n}\}$ in an abelian category $\mathfrak{U}$ is a collection of objects $C^{i},i\in \mathbb{Z}$ , and morphisms $d^{i} : C^{i} \rightarrow C^{i+1}$, such that $d^{i}\circ d^{i+1} = 0$. The morphisms $d=\{d^{i}\}$ are called the differential (or coboundary operator).

The $i$th cohomology object of the complex $\mathcal{C}$ is defined to be $H^{i}(\mathcal{C}) = \textrm{Ker }d^{i}/\textrm{Im }d^{i-1}$.

根据范畴的不同，我们可以定义上同调群、上同调模，接着就可以定义singular cohomology（奇异上同调）、de Rham cohomology（德拉姆上同调）、Galois cohomology（伽罗华上同调）、Čech cohomology （切赫上同调）等等。在集合论中，我们有类与集合的概念。所谓的类由所有享有共同性质的数学对象构成，但是它不一定是一个集合，如果它不是一个集合，我们称这个类是真类。接下来，我们给出Grothendieck universe 的定义，它是在上世纪由Grothendieck提出来的，用来避免不构成集合的真类。如果读者想要了解更多相关内容，可以参考[5], [6]。

Definition 3.2. A Grothendieck universe is a non-empty set $\mathcal{U}$ that satisfied the following conditions:

1. if $x\in \mathcal{U}$ and $y\in x$, then $y\in \mathcal{U}$.
2. if $x,y\in \mathcal{U}$, then $\{ x,y\}\in \mathcal{U}$.
3. if $x \in \mathcal{U}$, then $\mathcal{P}(x) \in \mathcal{U}$, where $\mathcal{P}(x)$ denotes the set of all subsets of $x$.
4. if $(x_{i},i\in I)$ is a family of elements of $\mathcal{U}$ and $I \in \mathcal{U}$, then $\bigcup_{i\in I}x_{i} \in \mathcal{U}$.

4. Modern Mathematics

以上内容其实都已经是以前发展的理论了，基本上都是20世纪的内容，已经有点旧了。接下来，我们讲一下21世纪比较新的内容：Shinichi Mochizuki和Peter Scholze的工作。

Shinichi Mochizuki(望月新一)就是那位声称证明了abc猜想的数学家，我们习惯叫他为望月大神。他刚开始主要是做hyperbolic curve相关的研究的，后来他开始通过运用自己以前的研究成果来研究远阿贝尔几何（anabelian geometry）。远阿贝尔几何最初是Grothendieck提出来的一个宏伟的理论，如今它被望月新一进一步发展，构建了一个名叫宇宙际理论（Inter-universal Teichmüller Theory）的东西，用于证明abc猜想，可惜世界上没有多少数学家能够看得懂他的证明，因此关于他的证明主流数学界仍不认可。

不同的是，Peter Scholze的工作则更为主流数学界所接受，很多人都更愿意做Peter Scholze的方向。Peter Scholze就是那个国际奥林匹克数学竞赛拿金牌，高中开始学习研究生数学的数学家，很年轻。在他的博士论文中，他发展出了一个叫状似完备空间（perfectoid spaces）的新东西，成为了当代算术几何最具影响力的数学家之一。

4.1. Rigid Geometry

Peter Scholze 所做的perfectoid spaces与刚性几何（Rigid Geometry）有关，接下来我们将对刚性几何的部分内容做介绍。想要了解更多的读者请参考[3], [4]。

首先我们需要研究非阿基米德的绝对值。对于与绝对值相关的valuation，在本文中我们将不予讨论。我们着重讨论非阿基米德的绝对值的特别之处。

Definition 4.1. A (non-archimedean) absolute value $\upsilon$ on a field $K$ is a map $\left| \cdot \right|$ : K $\rightarrow$ $\mathbb{R}_{\geq0}$, such that for all $x,y\in K$ the following conditions verified:

1. $\left| x \right|$ = 0 $\Leftrightarrow$ $x=0$.
2. $\left| xy \right|$ = $\left| x \right|$$\left| y \right|$
3. $\left| x+y \right| \leq \max\{\left| x \right|, \left| y \right|\}$

Proposition 4.2. Let $x,y\in K$, we have $\left| x+y \right|$ = $\max\{\left| x \right|, \left| y \right|\}$, if $\left| x \right| \neq \left| y \right|$.

Proof. Without loss of generality, we assume $\left| x \right| < \left| y \right|$. Then $\left| x+y \right|$ $<$ $\max\{\left| x \right|, \left| y \right|\}$ =$ \left| y \right|$ implies

$$\ \left| y \right| = \left| (y+x)-x \right| \leq \max\{\left| x+y \right|, \left| x \right|\} < \left| y \right|$$

which is contradictory. So we must have $\left| y \right| = \left| y+x \right| = \max\{\left| x \right|, \left| y \right|\}$ as claimed.

通过绝对值，我们定义任意域$K$上的距离为$d(x,y) = \left| x-y \right|$，然后该距离诱导出$K$上的一个拓扑。有了$K$中任意两点的距离，根据非阿基米德的三角不等式，对于所有$x,y,z \in K$，我们可以得出：

$$d(y,z) \leq \max\{d(x,y),d(x,z)\}$$

根据命题4.2，该不等式两边相等，如果不等式右边的两个距离不相等。这意味着：在域$K$中的任意三角形，都是等腰三角形。更进一步，我们可以证出：域$K$中任意一个圆盘中的点都可以作为该圆盘的中心。因此，如果$K$中的两个圆盘有非空交集，那么它们就是共心的。下面我们给出证明。

Definition 4.3. For a centre $a\in K$ and a radius $r\in \mathbb{R}_{> 0}$, we define the disk without boundary to be the set $$D^{-}(a,r) = \{ x \in K\mid d(x,a)<r \}$$

And we define the disk with boundary to be the set $$D^{+}(a,r) = \{ x \in K\mid d(x,a)\leq r\}$$

Proposition 4.4. Each point of disk without boundary in K is the centre of the disk.

Proof. Assume that $a$ is the centre of a disk, $b$ is a point different from $a$. For any $x\in D^{-}(a,r)$, we have $$ d(x,b) = \left| x-b \right| = \left| (x-a)+(a-b) \right| \leq \max\{\left| x-a \right|,\left| a-b \right|\} < r $$

类似的，我们可以证明对于有边界的圆盘，其中的任意一点都可以是它的中心。

4.2 Perfectoid Geometry

接下来我们粗略地说一下，Perfectoid spaces, [4]，这篇文章里面的一些内容，鉴于作者水平有限，不能一一详述。首先，perfectoid是perfect+oid，意思就是more or less perfect，类完美。

首先，我们回顾一下什么是完美域（perfect fields）。

Definition 4.5. Let $K$ be a field. We say that $K$ is perfect if either $K$ has characteristic $0$, or if $K$ has characteristic $p>0$, the Frobenius $$ \Phi:K\rightarrow K, x\mapsto x^{p}$$ is an isomorphism.

Perfectoid spaces这篇文章的动机源于以下Fontaine-Wintenberger的一个定理：

Theorem 4.6. The absolute Galois groups of $\mathbb{Q}_{p}(p^{1/p^{\infty}})$ and $\mathbb{F}_{p}((t))$ are canonically isomorphic.

Remark 4.7.

$$\mathbb{Q}_{p}(p^{1/p^{\infty}})=\lim_{\substack{\longrightarrow \\ n>0}}\mathbb{Q}_{p}(p^{1/p^{n}})=\bigcup_{n>0}\mathbb{Q}_{p}(p^{1/p^{n}}).$$

$\mathbb{Q}_{p}(p^{1/p^{\infty}})$是一个特征0的域，它的剩余类域$\mathbb{F}_{p}$是特征$p$，这种域被称为混合特征的（mixed characteristic）。而$\mathbb{F}_{p}((t))$ 是一个特征$p$的域。意思是如果将所有$X^{p^{n}}-p\in\mathbb{Q}_{p}[X]$的根加到$\mathbb{Q}_{p}$里面，它会看起来像一个特征$p$的域$\mathbb{F}_{p}((t))$。想要更好地理解$\mathbb{Q}_{p}(p^{1/p^{n}})$是什么意思，可以参考$\mathbb{C}\cong\mathbb{R}(i)\cong\mathbb{R}[X]/(X^{2}+1)$这个例子。同时，我们有这样一个tower:

$$\mathbb{Q}_{p}\subseteq \mathbb{Q}_{p}(p^{1/p})\subseteq \mathbb{Q}_{p}(p^{1/p^{2}})\subseteq \cdot\cdot\cdot \subseteq \mathbb{Q}_{p}(p^{1/p^{n}})\subseteq \cdot\cdot\cdot \subseteq \mathbb{Q}_{p}(p^{1/p^{\infty}}).$$

定理4.6可以在更加一般的框架下研究，这就引申出了perfectoid fields。 首先，我们给出非阿基米德域的定义，它其实就是一个拓扑由一个非阿基米德绝对值生成的拓扑域。

Definition 4.8. A non-archimedean field is a topological field $K$ whose topology is induced by a non-trivial valuation of rank 1.

Definition 4.9. A perfectoid field is a complete non-archimedean field $K$ with residue characteristic $p>0$ whose associated rank-1-valuation is non-discrete and the Frobenius $\Phi:K^{\circ}/p\rightarrow K^{\circ}/p,x\mapsto x^{p}$ is surjective.

Example 4.10. The $p$-adic completion $\widehat{\mathbb{Q}_{p}(p^{1/p^{\infty}})}$ of $\mathbb{Q}_{p}(p^{1/p^{\infty}})$ and the $t$-adic completion $\widehat{\mathbb{F}_{p}((t))(t^{1/p^{\infty}})}:=\mathbb{F}_{p}((t))((t^{1/p^{\infty}}))$ of $\mathbb{F}_{p}((t))(t^{1/p^{\infty}})$ are perfectoid fields.

$$\widehat{\mathbb{Q}_{p}(p^{1/p^{\infty}})}=\widehat{\mathbb{Z}_{p}[p^{1/p^{\infty}}]}[\frac{1}{p}]=(\lim_{\longleftarrow} \mathbb{Z}_{p}[p^{1/p^{\infty}}]/p^{n})[\frac{1}{p}],$$

$$\widehat{\mathbb{F}_{p}((t))(t^{1/p^{\infty}})}=\widehat{\mathbb{F}_{p}[t^{1/p^{\infty}}]}[\frac{1}{t}]=(\lim_{\longleftarrow} \mathbb{F}_{p}[t^{1/p^{\infty}}]/t^{n})[\frac{1}{t}].$$

Perfectoid field叫做类完美域，当它为特征$p$时，它是一个完美域。同时，这里有一个tilt的过程，它可以看成一个函子叫做tilt funtor:

$$K\mapsto K^{\flat}$$

将一个任意特征的perfectoid field打到一个特征$p$的perfectoid field。同时，我们有

$$K^{\flat}=\lim_{\substack{\longleftarrow \\ x\mapsto x^{p}}}K.$$

接着我们有了更加一般的定理，它推广了定理4.6。

Theorem 4.11. The absolute Galois groups of $K$ and $K^{\flat}$ are canonically isomorphic.

总之，这篇文章中，Peter Scholze提出一种框架，它能将任意特征的问题简化为特征$p$的问题，因为特征$p$往往更好研究，同时也有很多好的性质和结论。