把加法与乘法结构拆掉再复原？望月新一如何引发代数几何变革

据《朝日新闻》，望月新一关于ABC猜想的论文可能将要发表，审核它的期刊是《数理解析研究所公刊》（PRIMS）。

媒体对此的报道大抵聚焦在两点上：一是这个期刊就是他的工作单位主办的，一是这个论文几乎无人能懂。

作为一个数学研究者，我个人并不担心望月新一的利益冲突问题，不但因为数学界有一套相当完备的系统用以避免利益冲突，在选定编辑和审稿人时有良好的避嫌标准，更重要的是：他没有动机。他已经功成名就，不需要什么文章。数学这种东西，对就对，错就错，不存在编数据或者实验造假，一切细节都在文章里。要是错了，无论强行发表在什么期刊上，也终有一天会被发现，而一发现就无可抵赖，只能重新修补。

但是他的理论绝不仅仅是一个“几乎无人能懂”的怪物而已。它所试图解决的根本数学问题，它背后的当代数学界的面貌，它反映出的做数学研究是怎样的状态，这里面还有太多的故事并不是、也不应该是只有几个人能懂。

甚至也许可以说，这些故事能让人直观地感受到：现代数学是什么。

破题

望月新一的研究领域，是所谓的“远阿贝尔几何学”。如果一句话解释这个领域的话，我只能这样写：

有理数的绝对伽罗华群，以至任意代数簇的平展基本群，它们“远离阿贝尔”的部分，也就是不符合交换律ab=ba的部分，会如何影响相应代数结构的性质。

看不懂这句话是正常的。要解释这个领域研究的是什么，可能需要整整一篇文章（可以参看http://songshuhui.net/archives/96606），还不一定能解释清楚。而且那篇文章还得找一个远阿贝尔几何的专家，不是像我这样搞组合数学的人。

是的，对于望月新一的体系，我其实也只算理解基础，是数学界内部的吃瓜群众。但面对这个体系，很多数学家的境况并不比我好得多。包括菲尔兹奖得主陶哲轩，包括望月新一的恩师法尔廷斯，他们都抱怨望月新一的证明太简略太难懂。现在，懂得整个证明的，除了望月新一之外，据说只有十几个人，大部分在日本，其他在美国和法国。

但是，如果他是对的，那就意味着代数几何的重大革新。

一个人能够改变一个学科吗？

一个新的证明或者理论体系，给数学界带来重大影响，这并不是第一次。

大卫·希尔伯特也许是最重要的现代数学家之一，光是他在1900年提出的那23个数学问题就差不多贯穿了整个世纪。他的成名之作，那篇“终结了不变量理论”的论文，在当时就引起了巨大的争议。此前，不变量理论的大多数进展都基于具体的计算，需要给出具体的结果。这样的证明又叫构造性证明。但希尔伯特的证明不属此列，而分属“存在性证明”，能断言某个数学对象的确存在，但对于如何计算却绝口不提。他一开始投稿恰好碰上了当时的“不变量之王”哥尔丹。哥尔丹对这样的证明颇有微词，他的退稿评价是：

这不是数学，这是神学。

但最终希尔伯特幸得克莱因的保荐（“这无疑是这本杂志发表过有关一般代数的最重要的工作”），论文得以发表。正因为无需具体给出构造，存在性证明要比构造性证明要更为简洁有力，也因此逐渐被广泛接受。即使是一开始拒稿的哥尔丹，最后也承认了希尔伯特的工作，“即使是神学也有其价值”。希尔伯特之后也因为公理化的工作以及其他数学成就，跻身当时数学界的顶尖。

另一位为数学界作出巨大贡献的德国数学家康托尔，他的命运却大不相同。在研究傅里叶分析时，康托尔领会到无穷之后仍有无穷的无穷。他从最基础的集合论开始，建立了一个全新体系，描述了超越无穷的无穷，也就是超穷[songshuhui.net/archives/90745]。集合论中的很多基础结果，就出自他的手笔。

但他的研究甫一发表，就遭到许多顶尖数学家的攻讦。庞加莱说他的想法就像“严重的疾病”，正在感染数学这一学科。当时执德国数学界牛耳的克罗内克，公开反对康托尔关于超穷的理论，甚至到达了人身攻击的地步。他称康托尔为“科学骗子”、“背叛者”、“腐蚀了青年”，近乎偏执地指责着康托尔和他的理论。

但数学毕竟是数学。经过曲折发展之后，集合论成为了现代数学的基础，成了数学系学生的必修课。正是希尔伯特作出了这样的断言：

身处康托尔跟我们一道展开的天堂内，我们屏息于惊叹之中，知道无人能将我们由此驱逐。

可惜，康托尔本人的命运却远没有那么光明。也许是因为得不到理解，也许是因为这些无休止的攻击，康托尔患上了抑郁症，一直没有痊愈。他的晚年恰逢第一次世界大战，贫困加剧了战争带来的饥谨。心脏病给他的最后一击，也许是种解脱。

有好几个人把望月新一比作上一代的数学家格罗滕迪克。格罗滕迪克的遭遇处于康托尔和希尔伯特之间。他的数学风格高度抽象，但却能得出实际的结果。引用我之前写的：

他谈论的数学实在过于抽象，难以理解。但这就是格罗滕迪克做数学的风格：尽可能从数学对象中将不必要的细节抽象出来，抽象得一般的数学家都会以为剩下的只有“虚空”，然而他仍然能从“虚空”中抓住某些东西，从而建立他的理论，完成他的证明。用格罗滕迪克本人的说法，如果把数学问题比作坚果，大部分数学家做的就是用锤子和凿子把坚果凿开，而他的做法则是将坚果浸在水里，慢慢软化它的外壳，又或者让它经受风吹日晒，然后等待合适的时机，坚果自然就会裂开。

对于大部分数学家来说，这个过程太漫长，也许只有拥有深刻洞察力的格罗滕迪克，才能在能接受的时间内，用这种方法解决问题。这也是他的数学难以被理解的原因之一：他几乎不考虑具体的示例，都是从尽可能抽象的角度出发，思考支配某个数学问题背后的宏大数学结构。有时候这也会闹出笑话。有一次讨论数学的时候，有人向格罗滕迪克提议考虑一个特定的质数作为例子。“你的意思是找一个真实的数字？”格罗滕迪克有点疑惑。对方点了点头。他回答：“好吧，我们考虑57这个质数。”57当然不是质数，但格罗滕迪克大概没有注意这一点，他从来不考虑具体的例子，一切从抽象出发。

格罗滕迪克的这种风格，让他年纪轻轻就全套改写了代数几何所用的数学语言，给这个领域带来了全新的抽象思维方式，让代数几何成为数学中可能是最抽象最深奥但也最有力量的分支。他编写的EGA和SGA是代数几何的入门宝典，他的定理和想法，尤其是标准猜想，仍然留在众多代数几何学者的心头。

当然，新理论新证明被彻底摧毁的例子也比比皆是。在2004年，美国数学家路易·德·布朗奇（Louis de Branges）在自己的个人页面上贴出了一篇124页的论文，声称利用自己发展的基于希尔伯特空间的一套体系，证明了数论中最引人注目的黎曼猜想，跟望月新一的情况相当相似。因为德·布朗奇此前曾证明另一个著名猜想——比伯巴赫猜想（Bieberbach conjecture），所以也有人关注他的证明。但直至现在，论文经过多次修改，似乎仍然站不住脚。目前数学界普遍认为他并未能证明黎曼猜想。

不停有人提出新的想法，即使一开始不被接受，历经时间洗练，终将得到应有的评价，而数学也就此进步。虽然提出新想法的人，他们各自有需要承受的命运，不以他们的贡献为转移。这就是数学史。

而望月新一的理论，就是在当下展开的历史。他的理论是对是错，只能拭目以待。

抽象的极致

望月新一给他的体系起名为“宇宙際Teichmüller理論”（inter-universal Teichmüller theory），简称IUTT，有时候也省略对应“理论”的T，写成IUT。

他并没有特意发明这个略显中二气息的名字，这锅要由他的先驱格罗滕迪克（Grothendieck）来背，是他发明了Grothendieck universe这个数学对象。而universe这个术语可能还要追溯到更久远的集合论先驱，因为它对应着集合论中“所有集合组成的一堆东西”这个概念。是的，所有集合不构成一个集合，只能说成“一堆东西”，或者用“类”这个术语。幸好，中文对universe的标准翻译“全类”没有那么中二。用上这个翻译的话，中文可以写成“跨全类Teichmüller理论”。但为了原汁原味起见，我们后面还是用“宇宙”这个术语。因为，另一个universe的数学，总有些不一样。

有多不一样呢？

这里实在没有办法深入探讨望月的IUT理论，不过正好有一个合适的例子，是望月新一在此之前研究的一个最最基础的数学结构：p进整数。它并不在另一个universe，但你阅读它的感受，大概和数学家读IUT的感受类似吧。

p进整数是什么？对于数学家来说最快捷易懂的定义，就是：

对于素数p，$(\mathbb{Z}/p^n\mathbb{Z})_{n>0}$的投影极限

（懵了吗？我第一次看到这个定义时，一下子就读懂了——但是我读望月的论文，大概就是你现在的感受。）

p进整数有这样的一些特征（以p=7为例）：

......30211045064302335342 是一个7进整数。你没看错，省略号在前面，而且它不是无穷。

可以对p进整数进行“正常”的加减乘除。

1/5当然不是普通的整数，但它是一个7进整数：1/5 = ......5412541254125412

0的绝对值是0，1的绝对值是1，但2、3、4……的绝对值也是1，直到7的绝对值突然变成1/7. 然后，8、9、10……的绝对值是1，14的绝对值是1/7，依此类推，直到49的绝对值变成1/49……

如果根据这个绝对值定义将所有p进整数看成一个空间，它里面每个三角形都是锐角等腰三角形，而如果取一个球体的话，球体中每一个点都是球心。

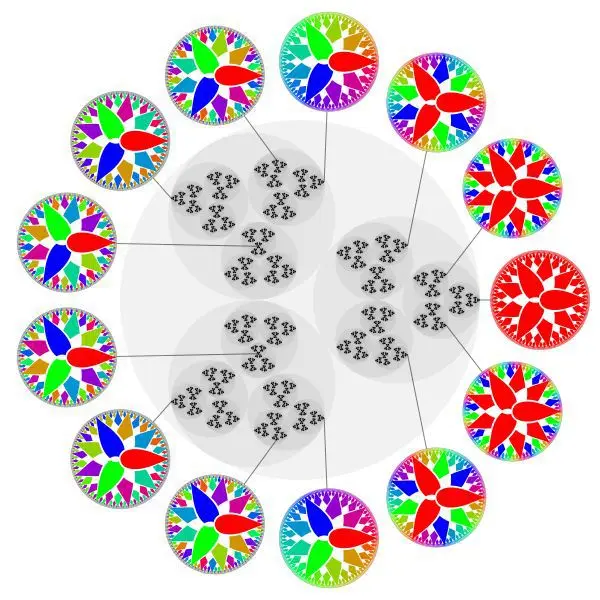图片来源：维基百科，作者Melchoir

图片来源：维基百科，作者Melchoir

一个自然的疑问是：这都是什么玩意儿？？？

有这种疑问很正常，因为这属于抽象而反直觉的数学。对于数学工作者来说，这种绝对值的定义，恰好呼应了p进整数本身的定义。如果明白一开始那个一句话定义，那么现在这个“绝对值”的概念，就会显得顺理成章，甚至非此不可。这就是对数学概念的理解程度所导致的偏差。初看似乎不明就里的数学概念，一旦掌握了正确的思维方法，就会变得浅显易懂。

但这又谈何容易！数学是如此抽象，必须经过多年的学习，慢慢熟习它的思考方式，才能理解它的内容。

p进整数，以及它的推广p进数，不仅在望月新一以往的工作出现，事实上，它早已是数论中常用的工具。当年怀尔斯对费马大定理的证明也用到了p进数。望月新一此前发展的p进Teichmüller理论，则完全基于p进数，但p进数本身在这个理论中的地位，相当于高考数学中的自然数，只是最基础的砖石。

而望月新一的新理论，“宇宙際Teichmüller理論”，还要高出一个层次。

他觉察到，用p进数构建的理论仍然不足以抓住他想要研究的那个数论结构，于是他另辟蹊径，找到一个已经证明必定能抓住那个结构的数学对象，然后构建起新的数学理论，研究这个对象的性质，从而导出他寻找的性质。这大体就是宇宙际Teichmüller理论的发展动机之一。

要构建这样的理论，需要同时用到远阿贝尔几何与表示论的工具，然而这两者格格不入，难以调和。为了折中，望月新一需要将理论的基底，也就是最基本的运算，拆成加法和乘法两部分，将它们消解为更复杂更抽象的结构，通过这些结构的互动和变形得到想要的性质，最后证明这些结构能够重新“復原”成某种加法和乘法。

在互动和变形的过程中，他要在不同的宇宙（universe、全类）间游走，才能得到足够广泛而一般的结论。加法和乘法结合起来会碰到的障碍，对于它们消解而成的结构却不成问题，当然前提是通过恰当的变形，就像不同坐标系之间的变换。这就是为什么望月新一要将他的理论称为“宇宙際Teichmüller理論”。顺带一提，消解后的加法和乘法面目全非，不像通常的加法和乘法那样基于同一套“数字”，而是形同陌路，望月新一的术语alien ring structure就由此而来。这里的alien，并不是什么“外星”的意思，而是取拉丁语alienus的原意“属于他人、非自身、外来、奇怪”之义。很多地方写的什么“外星算术全纯结构”（alien arithmetic holomorphic structure），都曲解了望月新一的本义。

看不懂？很正常。我自己的主要的研究领域是组合数学，虽然跟通常的Teichmüller理论有那么一丁点关系，但对于一般的代数几何我也没有正式学习过，所以只能在这里描绘它大致的图景。

但这就是现代的数学。它研究的内容如此广泛如此深入，一个分支上的数学家已经难以理解另一个分支的前沿，更何况是代数几何这一最抽象的领域中耕耘的人特别少的分支远阿贝尔几何，它的最前沿的推广呢？更何况这个理论是如此抽象，处理的又是如此根本的数学结果。可以说，拥有足够的知识储备，有充足时间能够理解并审查望月新一理论的数学家，即使不能说屈指可数，也很可能不超过100人，这还是相当乐观的估计。

望月新一本人这样说过，他的理论在数学界的处境，就像数学本身在整个社会中的处境：过于抽象，以至于人们不愿意去钻研和理解。

理论的渗流

虽然难以理解，但新理论的确有其吸引力。望月新一本人在代数几何这个领域早已名声在外，他在1996年就证明了格罗滕迪克提出的一个有关远阿贝尔几何的猜想，还因此被邀请在1998年的国际数学家大会上作45分钟演讲。既然他之前的工作证明了他有如此能力，那么他的新工作当然也值得认真对待。何况，望月新一宣称他的新理论能够用于证明数论中悬而未决的ABC猜想，这就更让人期待了。

有些数学家被新理论所吸引，花了大量时间研读，自觉理解了箇中真谛，成为了给新理论摇旗呐喊的人。

有些数学家同样被新理论说吸引，花了大量时间研读，但感觉还是解释不清，难以理解。

有些数学家对新理论有兴趣，但没有时间研读，只能交给别的专家。

有些数学家不懂这个分支，只能围观。

望月新一的“宇宙際Teichmüller理論”（IUTT），就这样将数学界分成了两大阵营：觉得自己读懂的，还有觉得自己没懂的。围观群众不在此列。

觉得自己读懂了的数学家，他们在积极地宣传这个理论，想让更多的人理解它。伊万·费先科就是其中一员。近年来，在世界各地召开了数次讨论IUTT的研讨会，费先科有不少牵线搭桥之功。他和其他数学家也撰写了不少介绍IUTT的文章和综述，试图用不同的视角来讲述这个理论。

觉得自己没有读懂的数学家，有的仍在努力研读，有的尝试用自己知道的数学方法来从侧面验证IUTT的正确性；也有的已经放弃，转而对IUTT的正确性产生了怀疑。

每个新理论都会经历这个阶段，这个等待验证的阶段。只有经过这个阶段，等到大部分专家接受它的正确性，新理论才算是正式确立，数学也得以进步。

只是，对于IUTT来说，这个阶段似乎太长了一点。

同样是代数几何中的新突破，另一位数学家彼得·索尔策（Peter Scholze）在2011年前后提出的perfectoid空间，很快就被数学界所承认，证据就是他从2012开始获得的一系列殊荣。要知道，他提出这个理论的时候还只是博士生，但在2012年答辩之后，没过多久就被母校波恩大学重新聘请为教授，以24岁的身份创下了德国史上最年轻教授的记录。熟悉德国教育系统的人，会更感叹他的成就，因为在德国，教授的地位很高，聘请的条件也因此非常苛刻。这更凸显了他的成就。

那么，索尔策和望月新一，两人的理论为何遭遇迥异？

索尔策的理论处于代数几何研究的主流，能理解的专家人数比较多，而望月新一的理论则不算主流，专家也比较少。有时候人多人少，也能决定理论被接纳的速度。索尔策的理论包含的新意，很快就能被读懂并应用到新的问题上；望月新一的IUTT则是全新的系统，略有格罗滕迪克的遗风，看起来波澜不惊，但结论出人意料，需要吃透整个系统，才能判断最后的证明是对是错，但过于浑然一体，也让别人难以进行旁敲侧击式的验证，偏偏这种验证也正是考验新理论最快的方法。

对于望月新一来说，这些都是非战之罪。虽有忮心，不怨飘瓦。

但望月新一自身也并非毫无责任。对于现代数学家的标准而言，他的个性也稍有乖张之处。即使他曾经在美国生活过，在回到日本之后，他就很不愿意到海外与其他数学家交流。他并非不乐意交流，证据就是在2016年的一次IUTT研讨会上，他曾通过视频通话接入会场，为与会数学家解答一些疑难问题。而他窝在京都长时间自己捣鼓这一套理论，也不是数学界通常的做法。一般来说，数学家至少会跟同一个实验室的同事讨论相关问题，在讨论之中，可以获得更多灵感，也能借此检验理论是否正确，或者投石问路，看看是此路不通还是大有可为。上一个口风像望月新一那么严的，还是证明了费马大定理的怀尔斯。当然，数学家经常开学术会议互相交流，少不免走漏风声。我当然不知道望月新一有没有跟同事讨论，很可能有但是同事的保密工作做得很好，也许没有但这个可能性很低，又或者关注远阿贝尔几何的人实在少。但结果就是，当这个证明出现之时，人们毫无心理准备。

另一个可商榷之处，就是他在公开他的理论时，没有选择数学界一般会使用的预印本网站arXiv，而是直接放到了自己的个人页面上。当然，论文放到什么地方，这是他的自由，但也使数学界不能及时了解他的理论。不过话又说回来，这项工作引起的轰动，也很快让他的论文为数学界所知，所以其实问题也不大。

可以说，他的个性或者说偏好，在客观上的确阻碍了他与同行之间的交流。

结果就是，现在即使接受IUTT的专家越来越多（对于一个相对冷门的领域来说，十几个专家不算少数），但这些专家相当一部分是望月新一在日本的同事，还有过从稍密的同行。当然，也有相对独立的学者认为他们同样搞懂了望月新一的证明，但人毕竟也会犯错，很多旁观的数学家认为，现在认同的人数还不够多。

数学这门学科虽然有无可辩驳的逻辑作为守门人，但它仍然是一种人类活动。新理论无论是对是错，总要有足够的人承认，才得以确立。确立后的理论也不一定正确，确立后被推翻的证明虽不多，但也有。只有当大部分专家都理解了这个理论，再也挑不出毛病，从而站到了“自认为懂”的阵营里，甚至能由此生发出新的结果，理论才算真正确立。没有相应专业知识，或者不肯花时间的人，都只是局外人，没有权利对理论的正误说三道四。

但事情毕竟在进展。据说，目前IUTT的四篇论文中，前两篇构建的体系已经被许多专家认为成立，即使是那些觉得没有读懂整个证明的专家。目前争议的焦点之一，在于第三篇论文的推论3.12，也就是Szpiro猜想的证明关键。Szpiro猜想能推出ABC猜想，也难怪大家特别关注这个推论。据说，在之前的版本，推论3.12的证明只有几行，语焉不详，但我看到的几天前（2017-12-14）的新版本中，望月新一加上了好几页的注解。我只能希望这些注解能消除某些专家的疑惑。

在伊万·费先科（Ivan Fesenko）的“科普”文章里提到，在关于望月新一证明的讨论中，有一个词经常被提到，就是“復原”。在望月新一构建的崭新数学体系中，他将同时附着在“数字”之上的加法结构和乘法结构拆开，将两者各自变形，然后重新“復原”。这种做法，先从根本上消解，之后再““復原”，即使对于久经抽象推理沙场的数学家而言也相当奇怪。而望月新一的体系，正系于这种“復原”的可行性。

如果他的体系是正确的，如果他的“復原”是成功的，这将带来数学中代数几何分支的变革。比如说，ABC猜想的证明。比如说，最终理解加法和乘法之间的关系。但现在，没多少数学家能读懂他的证明。无论证明是对是错，也许数学界，至少是代数几何，恐怕难以复原为以前的面貌。他的体系，他的证明，已经将数学家拆开成不同的阵营，阵营内部不断发酵变化，引出了新的分歧。即使最后尘埃落定，得到的恐怕也只是望月新一式的“復原”。

但这就是数学前进的必经之路。

后记

我一直觉得，写这篇文章的不应该是我。我做的是组合数学，代数几何只是外行，虽咨询了比我更懂的同事，但还是不敢说对它有足够的理解。

但了解更多的人在哪里？

我理解他们。这毕竟是一个高度抽象的学科，要向研究方向不同的同事解释尚且很有难度，更何况向一般人解释。

这也许也是望月新一不喜欢媒体的理由。媒体肯定不懂他的理论，只知道这可能是一个重大突破，可以搞个大新闻。但这些媒体何尝愿意了解他的理论？写成报道，焦点多半在个人的私生活上，要么就是各种八卦。看的人是很多，但看完之后，给人们又留下了什么教益？

但这个事情毕竟不能不做。正如他的新理论也需要知音来帮助宣讲，数学本身也要靠科普才能传播，人们才会认识到数学的重要性，而不是问出“微积分有什么用，又不能买菜”这种问题。怀有恶意的媒体固然会断章取义，但让更多人更了解数学的美妙也是件好事，值得再三权衡。

这篇文章，由于本人知识所限，难免有许多疏漏，权当抛砖引玉。希望与远阿贝尔几何关系更密切的专业人士，能写出更深入准确的文章，让大家分享数学最前沿的这一大事。

参考文献：