深度分析:为什么说没有外星人是很可怕的事?
人们对外星人总是很好奇,很狂热,其实这也很正常,毕竟人们内心深处总是倾向于一些陌生新鲜的事物,而外星人恰好满足了人们狂热的好奇心。

但另一方面,人们也对外星人充满了畏惧感,担心如果外星人造访地球,很可能给地球和人类带来毁灭性打击,甚至终结人类文明。尤其是在很多科幻小说和电影的渲染下,人们总是倾向认为外星人是很可怕的。
但或许我们大多数人都错了,真实的情况很可能是:发现外星人并不可怕,而如果没有外星人,才是最可怕的!
你可能会反驳:又在这瞎说了,没有外星人不是更好吗?就不会对人类有任何威胁了,人类也可以随心所欲地发展自己的文明,难道这不是更好的结果吗?
但我想说的是:那只是表象。如果没有外星人,如果宇宙只有人类,人类确实不用担心未来某天有外星人入侵的问题,但深入思考下去你会发现,事情远没有那么简单!
首先我们来分析一下,人类至今都没有发现外星人,但为什么绝大多数人都认为宇宙中一定存在外星人呢?

这个问题详细分析起来,其实是相当复杂的,但有一个共识:宇宙实在太大了!如此浩瀚的宇宙,从概率上分析,也不可能只有我们人类自己。
我们甚至不知道宇宙到底有多大!
就目前的科学探索发现,可观测宇宙直径大约930亿光年,可观测宇宙的外面是什么呢?

考虑到宇宙一直在超光速膨胀,几乎可以肯定:可观测宇宙的外面仍旧会是宇宙,只不过那里的宇宙与我们不会发生任何关系,因为那里发生的一切事情都与我们无关,信息完全不会传递到地球。
但即便是直径930亿光年的宇宙,对于人类来讲也几乎等同于无限大。可观测宇宙里拥有至少2000亿个星系,每个星系里都拥有上千亿颗恒星,而每颗恒星都拥有自己的行星系统。
这意味着,可观测宇宙里拥有几乎无限多颗行星。哪怕智慧生命出现的概率很低,有庞大的行星数量作为基数,智慧物种的数量也会是相当庞大的。
同时,考虑到宇宙长达138亿年的历史,在众多智慧物种当中,发展成为高级宇宙文明的概率也是很大的。理论上分析,一个足够发达的高级宇宙文明,应该早就遍布星系甚至宇宙的每个角落了。
但为什么人类至今都没有发现外星人的任何蛛丝马迹呢?为什么会出现如此矛盾的结果呢?

这其实也是著名物理学家费米感到困惑的问题,他在不经意间说了一句“他们都在哪里”,没想到后来经过“推波助澜”,成了著名的“费米悖论”。
对于费米悖论,之前我做了不少科普,对其进行了详细分析,这里就不再详述了,只想具体分析其中的一种解释:外星人并不存在!
这也是对费米悖论最“简单粗暴”也是最有效的解释,毕竟如果真的没有外星人,人们当然也就不可能发现外星人了。
但是,正如我刚开始所讲,虽然人类与外星人之间并没有什么关系,但如果宇宙中真的没有外星人,对人类的影响也会是“致命”的!

为什么这样说?可以用我们身边的事物和经历来理解。
在自然界,你能找到纯净的水吗?显然找不到。那么,如果一条鱼发现自己生活在纯净的水里,意味着什么呢?
或者也可以这样说,在一片巨大无比的茂密森林里,有一只小鸟,这只小鸟一直没有发现其他任何动物存在,这样的森林是不是很诡异?
伙伴们应该明白我想表达的意思。
如果没有外星人,我们人类就相当于那条鱼和那只鸟,对于人类来说,将意味着三种可能性:

第一,“大过滤器”会随时出现在人类文明发展进程中,把人类文明从宇宙中抹掉。
大过滤器理论其实已经被说“烂”了,虽然只是一个假说,但确实有很大的现实意义。如果没有外星人,有一种很大的可能就是智慧文明在发展过程中,到了某一阶段一定会遇到无法逾越的鸿沟,从而把智慧文明淘汰掉。
大自然就像筛子或者过滤器一样,任何智慧文明都无法逃脱。无法逾越的鸿沟可能来自文明内部,比如说文明内部的矛盾,文明发展的负面效应。也可能来自外部,比如说无法预测的超新星爆发等,可能瞬间导致宇宙文明终结。
那么,这也将意味着人类文明也一定会遇到“大过滤器”,我们不知道大过滤器什么时候到来,可能就在下一刻,就在明天,也可能在遥远的未来。但无论如何,结果都是:人类注定无法逃脱大自然的“筛选”!
一个形象的比喻是,智慧文明就像是宇宙的“癌细胞”一样,当发展到一定程度,上升到星际旅行阶段,就相当于癌细胞扩散,必然会被大自然无情地淘汰。
第二,人类生活的世界是虚拟的,对于这种观点,之前的科普文也做过详细分析,这里也不再详述了。

我想说的是,不要以为我们生活的世界真的是客观真实的,想想如今人工智能科技发展如此迅速,人类通过电脑能模拟出越来越多的真实场景,理论上分析,一个性能足够强大的电脑能模拟整个太阳系甚至银河系的真实场景。
换一种思维方式,人类又如何肯定我们自己生活的世界不是被更高级的智慧物种模拟出来的呢?
你可能会质疑:模拟这么大一个宇宙需要多大的电脑内存啊,根本不可能!
我想说:你多虑了!就像我们平时玩的电脑游戏那样,根本不需要把游戏的所有场景都模拟出来,只需要模拟渲染出游戏人物出现的场景,没有出现的场景根本不用渲染出来,只需要模糊化处理就可以了,这样就可以大大降低内存消耗。

说白了,人类可以“欺骗”电脑游戏里面的人物,让他们认为世界是真实的,毕竟他们看到的世界就是真实的(在他们眼里),他们没看到的世界虽然客观上是模糊的,不存在的,但是既然他们没有办法感知到其实也就相当于不存在!
而更高级的智慧物种同样也可以轻松“欺骗”人类,只需要模拟出人类能感知到的世界就可以了,感知不到的世界对于人类来讲其实就相当于不存在,当然不用渲染出来。
或许你打死都不愿意相信这个世界是虚拟的,毕竟我们看到的世界确实很真实。但想一想相对论和量子力学里面的诡异现象,如果用虚拟世界来解释,就轻松很多了。

比如说光速限制,或许就是高级智慧物种设定的虚拟世界加载极限,为了避免加载过快导致虚拟世界宕机!
还有量子力学中的不确定性,不观测时就是一片模糊的概率云,一旦人们实施了观测,就是确定的世界。这种现象不正是游戏世界里的基本规则吗:游戏人物出现的场景就会被确定地渲染出来,没有出现的场景就是模糊化处理状态!
第三,人类的出现就是概率极低的“错误事件”!
这种观点可能会让伙伴们的三观都崩塌了,因为在很多人的固有思维里,生命应该是朝着智慧的方向演化。
但其实不然,智慧并不是进化的方向和目标。如果你对地球生命进化史有详细了解的话,就会发现,智慧不但不是进化的方向,甚至是大自然非常讨厌的东西。

至于原因,简单说是因为“智慧太消耗能量了”,而简单的智慧在大自然根本发挥不了任何作用,把多余的能量提供给大脑提升智慧,远不如把能量提供给身体其他器官,来提升速度,力量,爆发力,灵活性等。
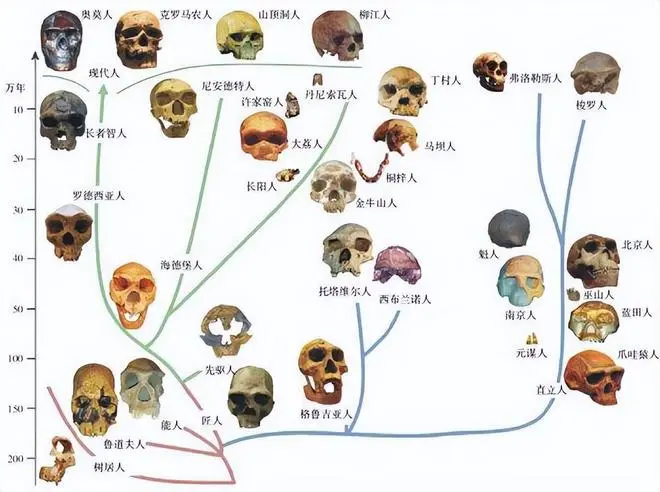
人类的远古祖先在漫长的进化道路上,其实进化出了很多人种,比如说海德堡人,格鲁吉亚人,蓝田人,元谋人,还有与智人生活在同时代的丹尼索瓦人,尼安德特人等,而所有这些人种最终都被大自然淘汰了,只有智人保留下来。
实际上,智人本应该也被淘汰,他们也确实屡次走在了灭绝的边缘,只不过智人足够幸运罢了。
关于大自然为何讨厌智慧,就说这么多,不展开了,否则就会延伸到有一个宏大的话题。总之,智人之所以能保留下来,完全是幸运。
往深了讲,人类的出现真的有可能是大自然出现的“错误”,一个概率极低的“错误”!而在人类漫长进化史上,任何一个微小的环节出现偏差,都会纠正大自然的“错误”,人类就不可能出现。
所以,不要以为人类是“天之骄子”了,或许我们根本就是一种“错误”!

总结
以上是我个人对于“没有发现外星人”的猜想,是在一定科学事实基础上做出的大胆猜想,或许某些观点太过偏激,触动了你基本的三观,我只能说抱歉了。
我科普的本意当然不是想“吓”伙伴们,只想拓展大家的思维,不要被日常固定模式束缚,大胆放飞我们的思想。
完!
0 人喜欢
暂无评论,来发布第一条评论吧!

