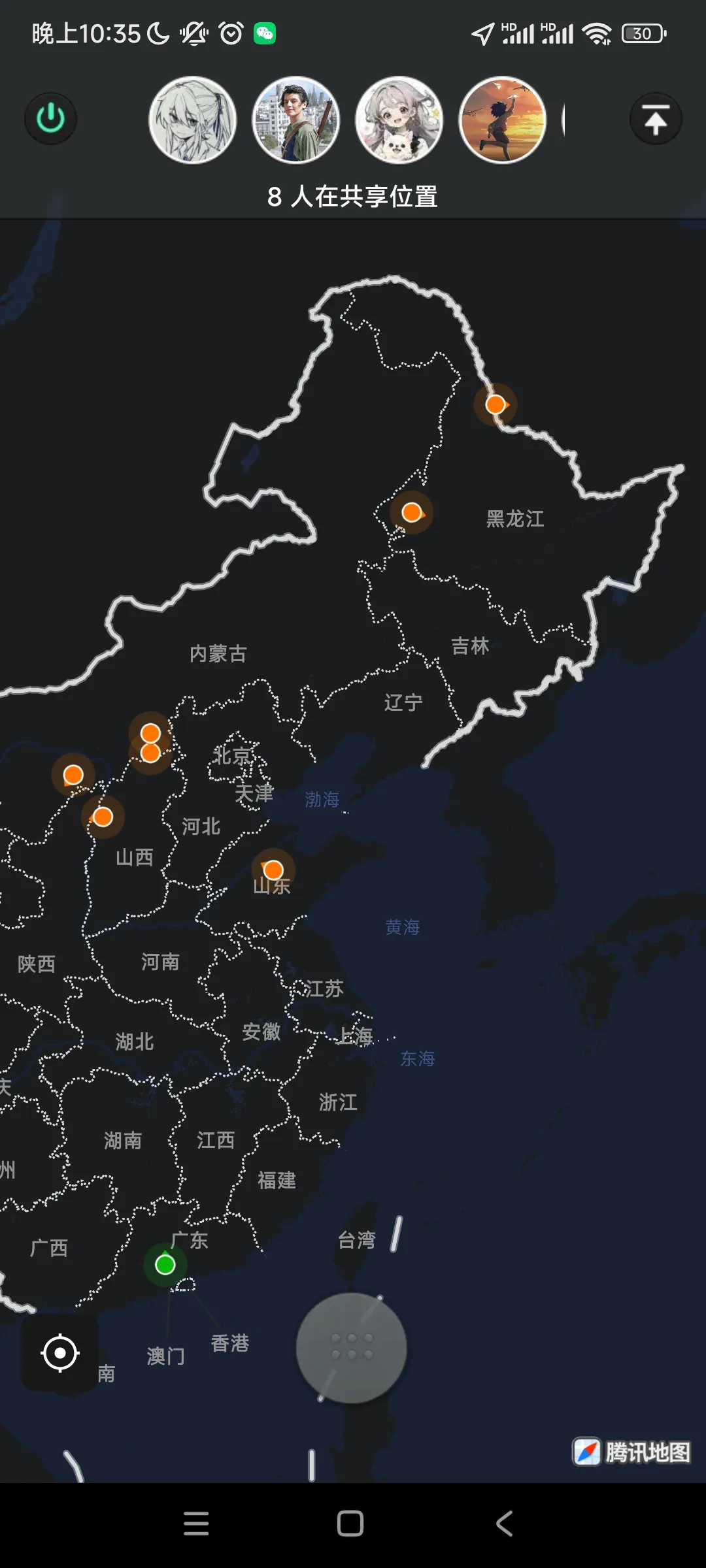
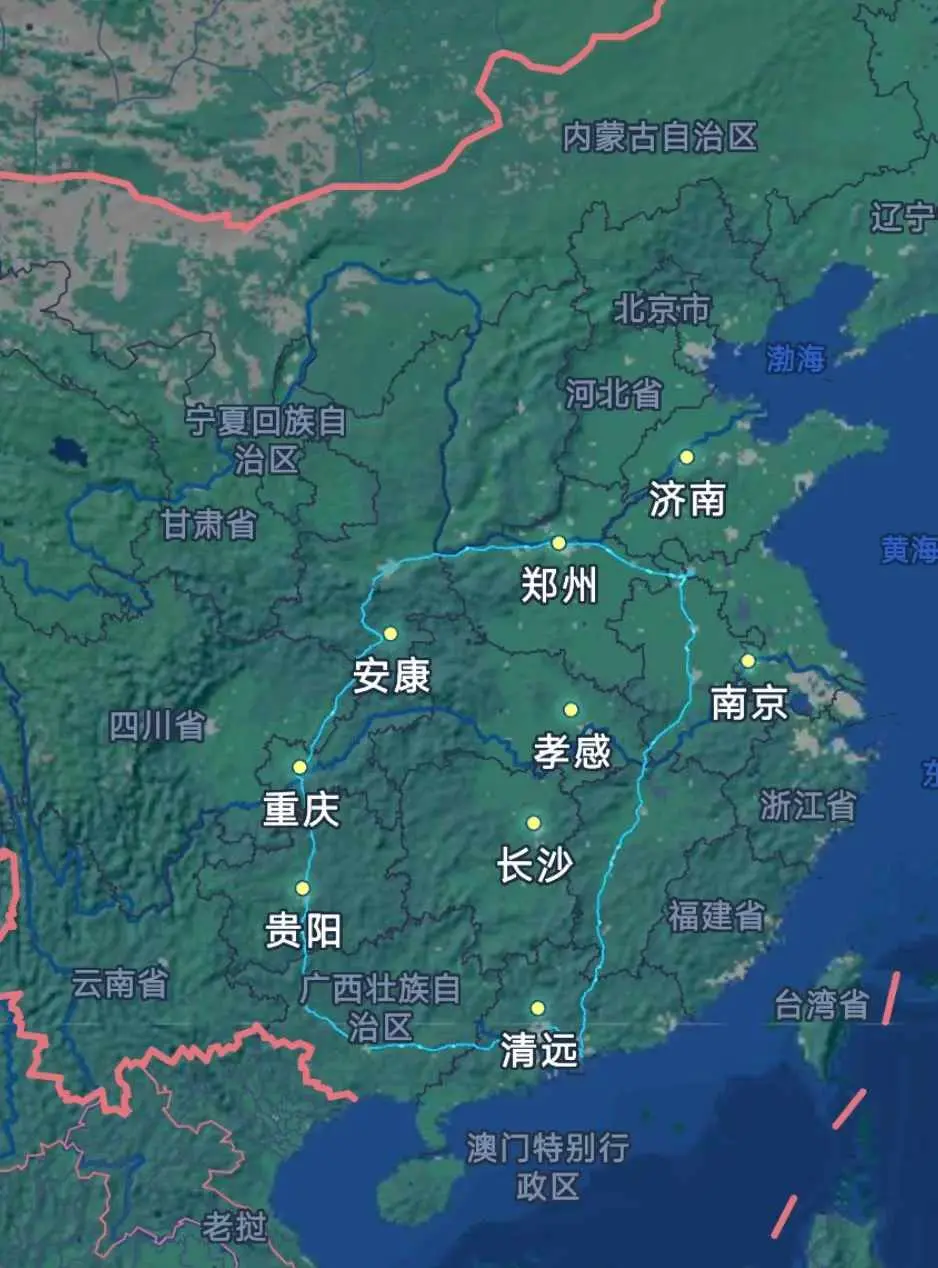
独行漫游指南
从8.8出发,8.29返深,约莫二十天,五千余公里,也算是一个人走过了小小半个中国。
1⃣️毕竟我是个没啥规划的人,很多事都是脑子一热就冲了。p3是出发前一晚楼下拍到的晚霞,心情不错,正好etc办好了,干脆就明天出发。说实话,出发前也觉得长途旅行是不是得置办点什么装备,但再等下去又要接着拖,就找最近的无印良品买了俩小布箱,放衣服行李。
2⃣️保险起见,热热身。
第二天早上买了包薯条就踏上了旅途,第一站先回广州,沈海高速熟得很,一阵子没开高速也算找找手感。广州熟得很,哪有好吃的哪有好玩的,游龙了两天,临走补充了矿泉水,薅了酒店的牙刷,直奔下一站。
3⃣️第一次正儿八经驾车出省。
虽然倒腾了一万多公里,多数是广州深圳来回,服务区都没进过几次。这下才知道,越往外走,越难走。到了肇庆云浮,虽是高速,但只剩下两条车道,应急车道经常有占道,两边是野草,路并不平整。常经过村落,远处的山平整延绵。
这里的充电桩建设是整趟行程最差的,服务区大多是国网桩,功率只有60kw,数量少,环境差。后来导航引导下高速充电,体验反而比服务区好很多,也就多绕个十分钟吧,但算上排队和充电速度也差不多。
3⃣️第一次在荒郊野岭开夜车。
黑。没有一丁点光照,前后很少有其他车,对向车道的远光更加加重了黑的感觉,除了自己车灯打亮的一小块地,两边只觉得黑压压的有什么东西,但总是看不清,偶尔经过建筑,那种黑夜中的朦胧感,会给人一种巨物恐惧的感觉。在这种相对自然的地方,体型也许是最大的压迫感来源。
4⃣️接近云贵川
从两广北上,山被一点点拔出了尖,各自独立,不再相连成一片。两广地区的山是一片一片的,而这边是一座一座的。于是就有了翻过一座山,背后又是一座山的感觉。
进贵州的地势不断拔高,电耗会尤其高,好在贵州高速建设的非常好,服务区漂亮的像小庄园,除了少数大型服务区,你都可以找到空闲的120kw充电桩,并且环境干净。
5⃣️山城下马威
离开贵州继续北上,山体裸露岩石的部分不断增加,当你看见这些石头山,路变得蜿蜒,隧道连着隧道,那便可以确定你来到了川渝。
这里的高速大多限速100-110,且有小半的路全是限速80的隧道,开得慢会有人滴你,但开到90就会和我一样收到超速11%警告短信。
重庆真是坐好城市,放松,热情,可动可静,我爱重庆,只是这里真的不适合自驾。堵车不说,即使是大型商场也无比难停车,并且在每一个合流车道,你都得进行不止一次的加塞博弈,这里的车一定会和你干到底的。
6⃣️向东
去西安的路要比进川好走的多,沿途除了山,也是有了点别的景色。但这一趟也跑出了两个问题,一是没有准备足够的东西路上听,二是没准备些方便食品。陕西的服务区建设确实不好评价,充电桩管够,第一次见服务区一排二十几根桩子,但服务区也是真的破,完全是年久失修。然而那天是8.20,赶路太晚加上猴瘾犯了,就在服务区玩了会睡觉,早上洗漱吃饭体验真的很差。
7⃣️出了西安,一切又好起来了。
北方服务区,理想和蔚来的桩是真多,都能拉到150-200kw(xp自己的桩充才140kw,幽默)。这边服务区才叫真的有服务,甚至简餐都算得上不难吃了,厕所也干净,停车场也整洁。
8⃣️船新体验,服务区也能卷?
这我是真没想到。路过合肥,一个服务区整得跟万达广场一样。从外看像机场航站楼,进去了完全就是大商场,外面有足足四个充电站,每个站8根桩以上,理想蔚来国网还有的挑,美美睡了一夜。说实话,要是服务区都这么好,我真愿意天天自驾游。
华东的景色就是一望无际的平原了,车道也是真的宽,基本是4车道,这里的风车很多,路上也是第一回见着活的运扇叶车。那玩意就聪身边经过,是真的大啊,好大好大,三辆半挂那么长,也很高。
9⃣️辅助驾驶好用吗
智能驾驶里程4335km,占比80%。每座城市都试过,基本都做的不错了,但高速全是智驾,到了城市还是手痒痒自己开爽。
回来的时候,大广高速有一大段施工路段,开不了辅助驾驶,我自己人开了俩小时,小两百公里,给我累的够呛,然后才是真的感觉到,这一路要是没辅助驾驶,我一个人真开不下来。







0 人喜欢
There is no comment, let's add the first one.