·
RicciflowsRicciflows

JS高级使用3.0——JS中获取页面的高度、距离顶部的距离

Published at 2024-08-28 00:15:22Viewed 205 times
Professional article
Please reprint with source link

创作场景

   记录闭包的博客中有一个节流函数的实际用法和这个知识点相关，创作过程中发现这个知识点涉及到的还有很多，在此记录一下相关的所有知识点并进行比较。

阅读前提

   此博客适用于所有人群，不仅有基础的用法，同时也对多种实现方式进行比较，本文将围绕一个例子进行讲解，并对涉及到的所有知识点进行穿插，最后进行总结。

提前了解的知识点

1. 页面可视化高度（clientHeight）

   页面可视化高度指的是你当前页面能看到内容的高度，这个高度是可以动态变化的，比如你打开了F12调试器，那么你的可视化高度就会变化，如果你将浏览器最大化，那么你的可视化高度也会变化，但这并不代表你实际页面的高度，可能你的页面高度会远远超过页面可视化高度。代码实现：

document.body.clientHeight

2. 滚动条高度（scrollHeight）

   滚动条高度就是当你的页面高度超过了页面可视化高度，比如body的高度是900，你的页面高度是800，那么滚动条就会产生，一般来说，滚动条高度是比你的页面高度要大16px，可能不同设备会不一样。代码实现：

document.body.scrollHeight

统计距离页面顶部的距离

参考：https://blog.csdn.net/mouday/article/details/125444003

  // 滚动方向枚举值
  const DIRECTION_ENUM = {
    DOWN: "down",
    UP: "up",
  };

   // 距离顶部或底部的阈值，一般滚动条高度是要比页面高度大的，阈值指的就是大的这一点儿
  const threshold = 20;
  // 记录前一个滚动位置
  let beforeScrollTop = 0;
  function handleScroll() {
    // 距顶部
    var scrollTop =
            document.documentElement.scrollTop || document.body.scrollTop 
            || window.pageYOffset || window.scrollY;
    // 可视区高度
    var clientHeight =
            document.documentElement.clientHeight || document.body.clientHeight;
    // 滚动条总高度
    var scrollHeight =
            document.documentElement.scrollHeight || document.body.scrollHeight;

    // 打印数值，console.table是控制台打印表格的写法，同时也有
    // console.error和console.warn，对应警告和错误
    // 一般使用的就是console.info
    console.table([
      {
        label: "距顶部",
        value: scrollTop,
      },
      {
        label: "可视区高度",
        value: clientHeight,
      },
      {
        label: "滚动条总高度",
        value: scrollHeight,
      },
      {
        label: "距顶部 + 可视区高度",
        value: scrollTop + clientHeight,
      },
    ]);

    // 确定滚动方向
    let direction = DIRECTION_ENUM.DOWN;
    if (beforeScrollTop > scrollTop) {
      direction = DIRECTION_ENUM.UP;
    }

    // 通过滚动方向判断是触底还是触顶
    if (direction == DIRECTION_ENUM.DOWN) {
      // 滚动触底
      if (scrollTop + clientHeight + threshold >= scrollHeight) {
        console.log("滚动触底");
      }
    } else {
      // 滚动到顶部
      if (scrollTop <= threshold) {
        console.log("滚动到顶部");
      }
    }

    beforeScrollTop = scrollTop;
  }
  window.addEventListener('scroll', handleScroll)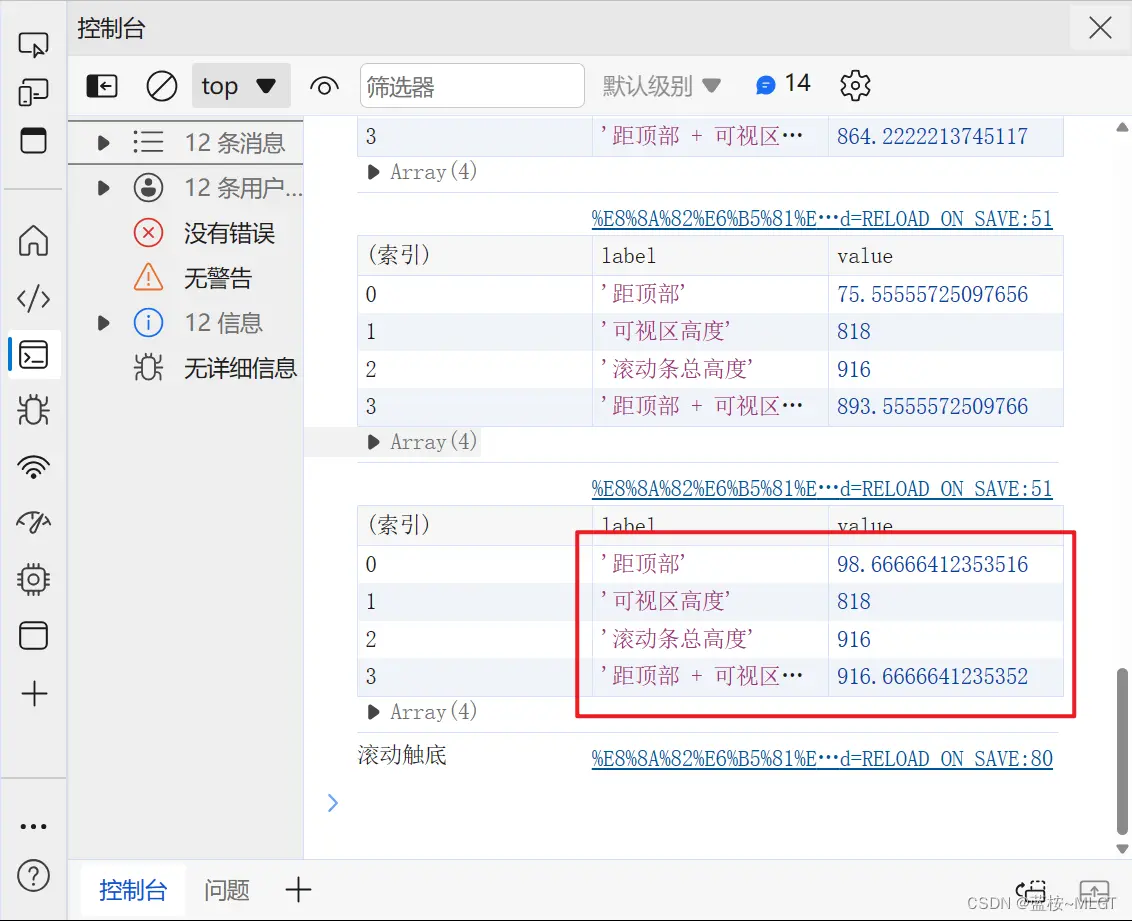

window、document、documentElement的区别

window是当前页面的顶级对象，其中包含了很多属性和方法，是一个BOM对象，可进行浏览器的交互。
document是window对象的子元素，它可以理解为一个DOM对象，其中有很多方法和属性，主要是在页面元素中进行交互。

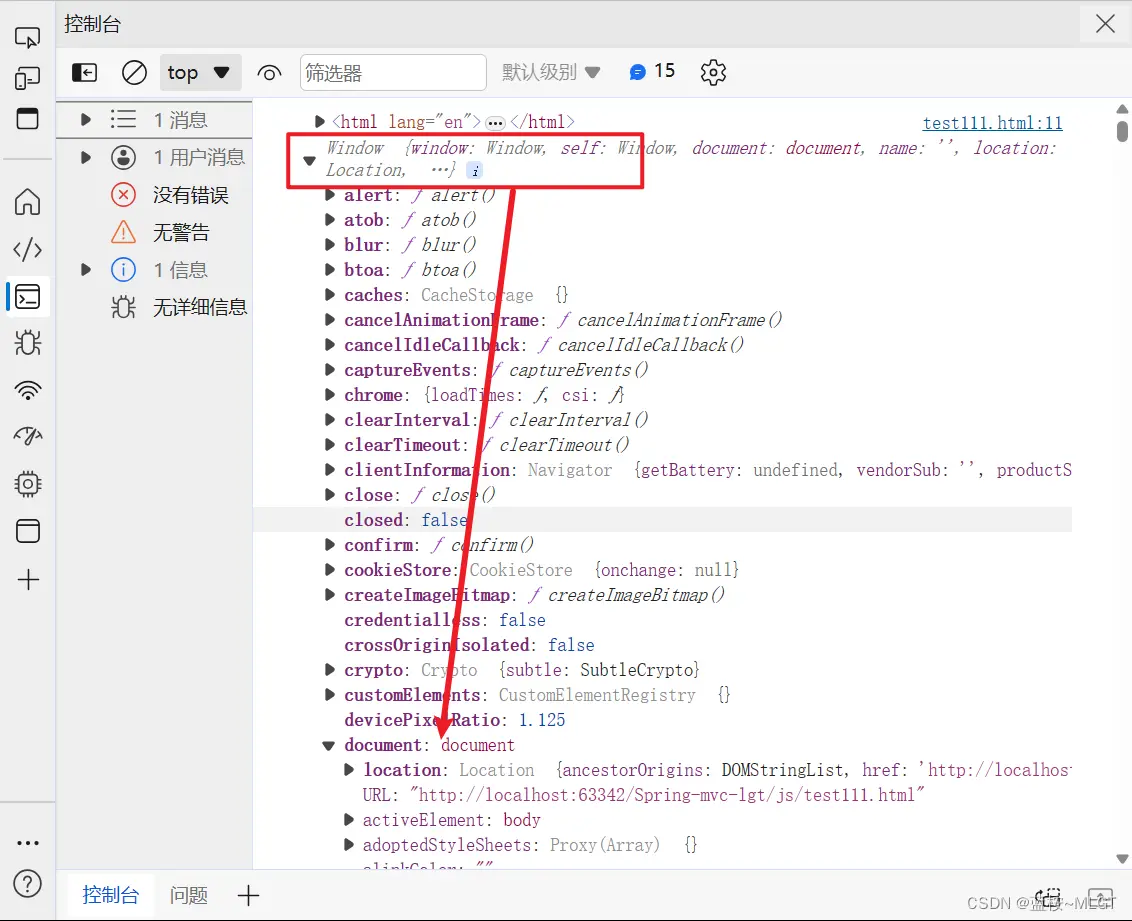
documentElement是document的子元素，注意，这是一个只读对象，也就是说它只能读取元素的属性，不能对元素进行操作。一般他就是你本页面的HTML元素。

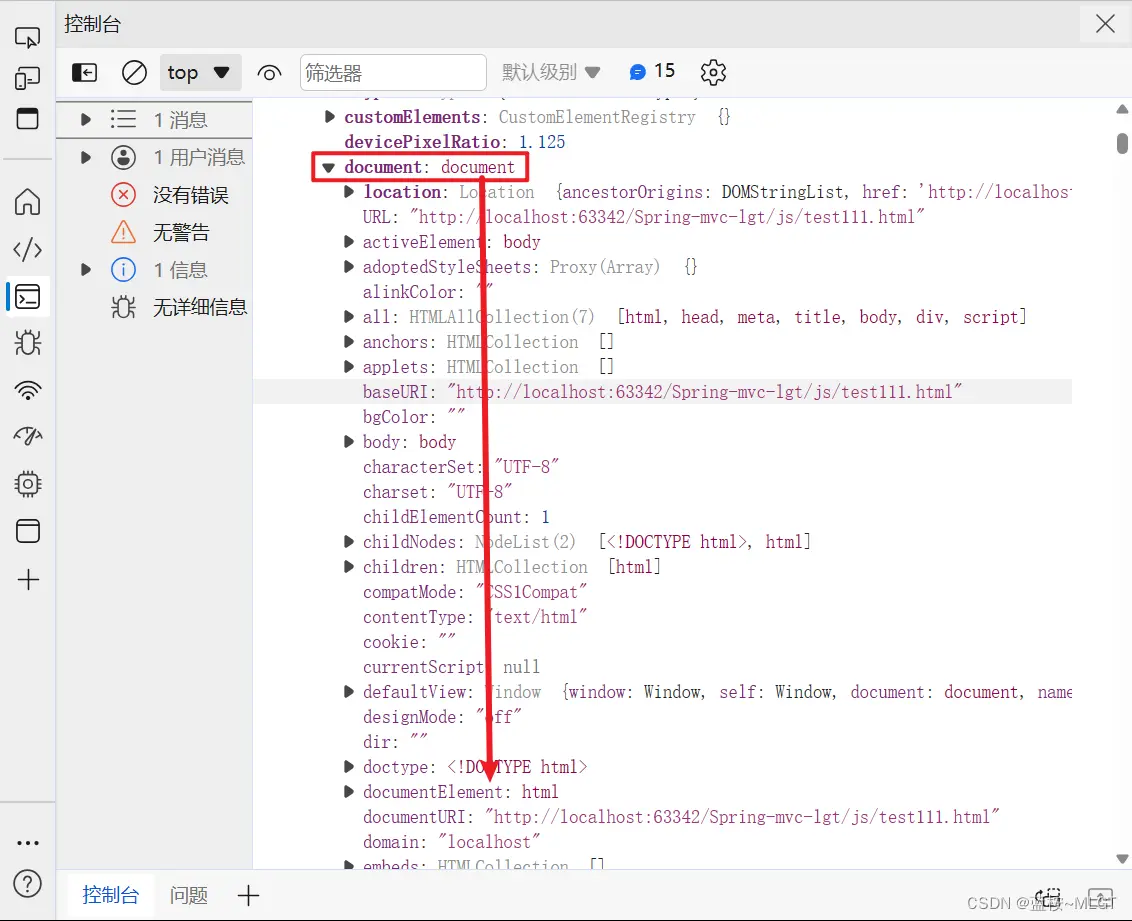
这里一定要注意一下，如果你的页面是在一个iframe中，那你获取的一定是你iframe中的所有元素，并不是你最大页面的对象。一般在实际开发中都有头部导航栏，而子页面中也会嵌套子页面，那么获取最外部的HTML元素可以用parent对象，一层一层循环，因为最外部的iframe肯定是有一个ID的，这是我在开发中遇到的一个小问题，分享一下。

// 第一个参数是当前的iframe对象，第二个是parent对象
// 调用时parentNode不用传入
function getFrameTop(frame, parentNode) {
	if (frame.attr('id') !== "iframeContent") {
		if (parentNode) {
			frame = parentNode.parent.$("iframe")
		} else {
			frame = parent.$("iframe")
		}
		getFrameTop(frame, parent)
	} else {
		topIframe = frame
		return frame
	}
}

解读获取距离页面顶部距离的四种方式

    // 距顶部
    var scrollTop =
            document.documentElement.scrollTop || document.body.scrollTop 
            || window.pageYOffset || window.scrollY;

  这四种拆分下来就是在两个对象上进行操作的，一个是window，一个是document，而之所以这么写完全是为了兼容性，尤其是pageYOffset方法，这是一个过时方法，但是在某些IE就只能识别这个，如果你的产品不需要兼容，那其中一个就够用了。

   解读一下原理：

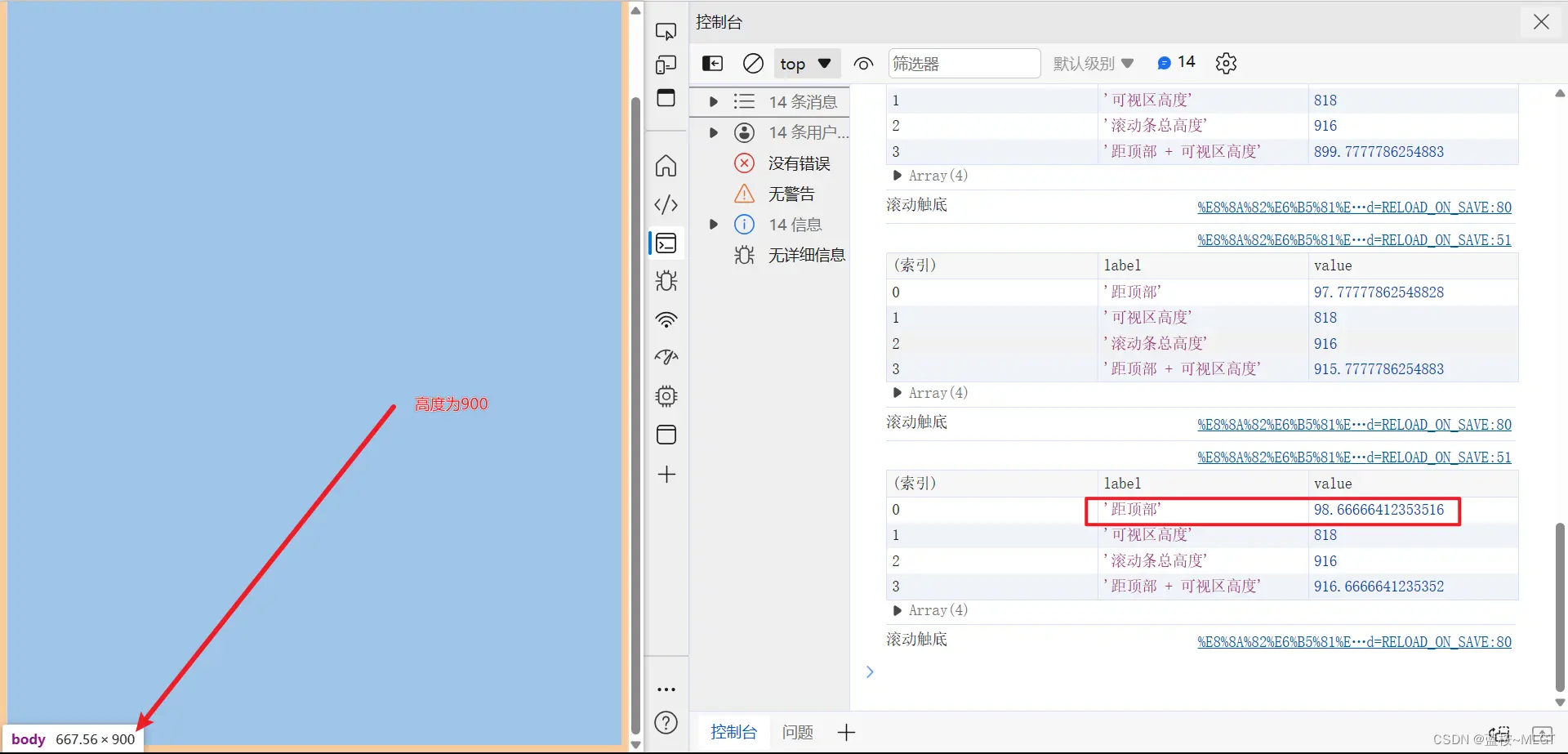
   我的div高度是900，页面可视化高度是818，而距离顶部的距离（scrollTop）是98，这其实就是滚动条的高度减去可视区高度算出来的，而这个高度指的是你的div最顶部距离和你可视化页面的顶部距离，如果是计算底部的距离，那加上页面可视化距离即可。

如何使用代码滚动页面（四种方式）

1. scroll()方法

滚动窗口至文档中的特定位置。
window.scroll(x, y) x和y就是你需要滚动的绝对位置坐标
window.scroll(options) options是一个对象，包含x、y坐标，同时也有滚动的方式
window.scroll({
  top: 100,
  left: 100,
  behavior: "smooth",
});

   上面这是一种标准用法，当然一般我们不这么写，直接用第一种方式滚动即可。

2. scrollBy()方法

在窗口中按指定的偏移量滚动文档（比如你只是想在这个基础上向下滚动100px）
scrollBy(x-coord, y-coord)
scrollBy(options)
x-coord 是你想滚动的水平像素值。
y-coord 是你想滚动的垂直像素值。
options
   包含以下参数的字典
top
   指定沿 Y 轴滚动窗口或元素的像素数。
left
   指定沿 X 轴滚动窗口或元素的像素数。
behavior
   指定滚动是否应该平滑（smooth）、瞬时运动到该位置（instant）、或者让浏览器选择（auto，默认）。
window.scrollBy({
  top: 100,
  left: 100,
  behavior: "smooth",
});

   这个方法和scroll区别在于，这里的x和y指的是偏移量，而不是绝对位置。

3. scrollTo()

   这个和scroll方法是一样的，个人比较喜欢这种方式，因为可读性比较高，不容易出错，使用标准写法可以随意在x和y上进行随意滚动，因为对象上参数可选。

// 设置滚动行为改为平滑的滚动
window.scrollTo({
    top: 1000,
    behavior: "smooth"
});

4. document.documentElement.scrollTop = 0（非标准写法）

   上面说过documentElement是一个只读属性，官方上也是这么说的，但是经过实验发现这种方式也可以用来操作页面的滚动，但不建议这么使用，也不知道会存在什么bug。

使用节流函数优化

关于节流函数是什么，这个博客中有说明

节流函数（闭包中的使用）
  function throttle(func, wait){
    let previous = 0;
    return function() {
      var now = Date.now()
      var context = this
      // ES5写法：var args = []; args.push.apply(null, arguments)
      var args = [...arguments]	// ES6数组解构知识点：复制数组
      // 如果当前时间减去上一次执行时间大于我们执行函数的时间间隔再执行
      if(now - previous > wait){
        func.apply(context, args);
        // 闭包，记录本次执行时间戳
        // 这么写就是不用将上次执行的时间作为参数传给函数了
        // 就算多次调用闭包不会消失，上一次执行时间不会消失，这就是闭包的常用方式
        previous = now;
      }
    }
  }
  // 滚动方向枚举值
  const DIRECTION_ENUM = {
    DOWN: "down",
    UP: "up",
  };

  // 距离顶部或底部的阈值，一般滚动条高度是要比页面高度大的，阈值指的就是大的这一点儿
  const threshold = 20;
  // 记录前一个滚动位置
  let beforeScrollTop = 0;
  function handleScroll() {
    // 距顶部
    var scrollTop =
            document.documentElement.scrollTop || document.body.scrollTop || window.pageYOffset || window.scrollY;
    // 可视区高度
    var clientHeight =
            document.documentElement.clientHeight || document.body.clientHeight;
    // 滚动条总高度
    var scrollHeight =
            document.documentElement.scrollHeight || document.body.scrollHeight;
    // 打印数值
    console.table([
      {
        label: "距顶部",
        value: scrollTop,
      },
      {
        label: "可视区高度",
        value: clientHeight,
      },
      {
        label: "滚动条总高度",
        value: scrollHeight,
      },
      {
        label: "距顶部 + 可视区高度",
        value: scrollTop + clientHeight,
      },
    ]);

    // 确定滚动方向
    let direction = DIRECTION_ENUM.DOWN;
    if (beforeScrollTop > scrollTop) {
      direction = DIRECTION_ENUM.UP;
    }

    // 通过滚动方向判断是触底还是触顶
    if (direction == DIRECTION_ENUM.DOWN) {
      // 滚动触底
      if (scrollTop + clientHeight + threshold >= scrollHeight) {
        console.log("滚动触底");
      }
    } else {
      // 滚动到顶部
      if (scrollTop <= threshold) {
        console.log("滚动到顶部");
      }
    }

    beforeScrollTop = scrollTop;
  }
  // window.addEventListener('scroll', handleScroll)
  window.addEventListener('scroll', throttle(handleScroll, 200))

这里只是一个例子，请注意，如果想要绝对精度，也就是当滚动条快速滑动的时候也要监听到，那就将延迟设置为0-50内。

总结

获取距离顶部的距离

  • document.documentElement.scrollTop
  • document.body.scrollTop
  • window.pageYOffset
  • window.scrollY

可视区高度

  • document.documentElement.clientHeight
  • document.body.clientHeight

滚动条总高度

  • document.documentElement.scrollHeight
  • document.body.scrollHeight

滚动页面

  • scroll()
  • scrollTo()
  • scrollBy()
  • document.documentElement.scrollY = 100


原文链接：https://blog.csdn.net/weixin_48588897/article/details/138413621

0 人喜欢

Comments

There is no comment, let's add the first one.

弦圈热门内容

把加法与乘法结构拆掉再复原？望月新一如何引发代数几何变革

据《朝日新闻》，望月新一关于ABC猜想的论文可能将要发表，审核它的期刊是《数理解析研究所公刊》（PRIMS）。媒体对此的报道大抵聚焦在两点上：一是这个期刊就是他的工作单位主办的，一是这个论文几乎无人能懂。作为一个数学研究者，我个人并不担心望月新一的利益冲突问题，不但因为数学界有一套相当完备的系统用以避免利益冲突，在选定编辑和审稿人时有良好的避嫌标准，更重要的是：他没有动机。他已经功成名就，不需要什么文章。数学这种东西，对就对，错就错，不存在编数据或者实验造假，一切细节都在文章里。要是错了，无论强行发表在什么期刊上，也终有一天会被发现，而一发现就无可抵赖，只能重新修补。但是他的理论绝不仅仅是一个“几乎无人能懂”的怪物而已。它所试图解决的根本数学问题，它背后的当代数学界的面貌，它反映出的做数学研究是怎样的状态，这里面还有太多的故事并不是、也不应该是只有几个人能懂。甚至也许可以说，这些故事能让人直观地感受到：现代数学是什么。破题望月新一的研究领域，是所谓的“远阿贝尔几何学”。如果一句话解释这个领域的话，我只能这样写：有理数的绝对伽罗华群，以至任意代数簇的平展基本群，它们“远离阿贝尔”的部分， ...

将反向传递看成函子：强化学习的一个复合视角

这篇文章是数学家与计算机科学家合作写的，将范畴论应用于人工智能的强化学习。本文表示，强化学习算法与强化学习算法的复合，还是一个强化学习算法，因而所有强化学习算法构成一个范畴$\textrm{Learn}$。然后在$\textrm{Learn}$里考虑神经网络，并证明在一般情况下，梯度下降也是复合的。如果对纯数学理论，在计算机或者AI有什么应用感兴趣的人，可以看看。我当时下这篇文章，也是好奇代数领域在AI方面有啥应用，其实当时已经知道有个叫热带几何（Tropical Geometry）的领域，就是代数几何在计算机的应用。因为当时AI就很火，但AI可解释性需要很多数学来解决，他们解决不了，所以我留着这篇文章也是打算之后写篇类似的AI应用的文章。

Tammo Tom Dieck代数拓扑教材

EMS出版的代数拓扑教材Algebraic Topology，作者是Tammo Tom Dieck。本教材相较于Hatcher的书，没有那么太多的插图，并且内容更加抽象。本书知识密度高，内容精炼简洁，没有过多的废话。很适合有一定代数基础，且喜欢直接切入主题，快速学习的人。对于还未入门的小白而言，这本书不太适合作为代数拓扑的入门教材。我高中的时候就在看这本教材，但总在一些地方无法彻底理解。但这本教材吸引我的地方，一是它的内容涵盖面够广，并且知识密度够高，能够让我短时间内掌握代数拓扑方面的基础知识；二是它的描述更加的抽象，并且语句简洁明了、容易理解，很符合我的口味（这也是我当时选择代数几何的原因）。关于本教材与其他代数拓扑教材更具体、更专业的对比，请看Algebraic Topology I: 对教材跟概念的一些论述。PS：作者不再提供附件下载。

望月新一关于abc猜想的天书证明：宇宙际Teichmüller理论

望月新一以及他的Inter-universal Teichmüller Theory（宇宙际Teichmüller理论）可以说是非常出名，相较于费马大定理证明的晦涩难懂，宇宙际Teichmüller理论才算是真正的天书，全世界没几个人能看得懂，就连大佬Faltings都看不懂。望月新一是Faltings的学生，Faltings以“暴力横推”的风格闻名，张寿武说过Faltings的风格就像直接开着推土机把山碾平了过去。并且Faltings看论文都是只看前沿（introduction）就能知道整篇论文的主要定理，甚至还能直接证出来。见望月新一与他天书般的论文，展现了纯数学与我们的距离可见Inter-universal Teichmüller Theory有多难懂，它涉及到代数几何一个高深的领域：远阿贝尔几何（anabelian geometry），顾名思义就是考虑平展基本群$\pi_{1}^{et}(X,x)$远离阿贝尔的部分，远阿贝尔几何源于Grothendick的一封入职信Esquisse d'un Programme，他于其中提出一个宏大的理论，然而最终他却没能将其实现。而望月新一可 ...

Algebraic Topology I: 对教材跟概念的一些论述

关键词：Homotopy, Homology, Groupoid, Foundamental Group, Van Kampen Theorem, Covering Space, Covering Projection, Fibration with unique path lifting, Cofibration.Tammo tom Dieck 在他的代数拓扑教材中写了非常漂亮的前言，在点出代数拓扑精髓的同时还包含一些形而上学的哲思，并且简略地介绍了代数拓扑里面的两个核心词汇，同伦(homotopy) 跟同调 (homology)。我简要地部分翻译如下：代数拓扑是连续数学跟离散数学交相辉映的学科。在连续数学里面，我们用拓扑空间和连续映射这样普遍的形式语言将其公理化。而离散数学则是被我们用来表达代数和组合概念的。在数学语言中，我们用实数来概念化连续形式，但我们建立实数时却是要用到整数。下面举个例子，我们直觉地认为时间是一个连续的没有间断的流动过程，是由一系列不停止的瞬间后继构成的。但在实践中，我们却使用被定义为有周期性的离散模型工具跟自然过程。同样地，我们意识到空间是一个连续体，但我们 ...

怀尔斯的费马大定理证明

费马大定理的证明可以说是算术几何的一个重要里程碑，当年怀尔斯虽然很小的时候就被该问题所吸引，从而选择做一个数学家。但作为一个这么多年都无人能破解的难题，怀尔斯也是兜兜转转，他也没一开始就打算攻克这个猜想。据说，是代数几何取得突破性进展之后，他才觉得是时候攻克费马大定理了。最后他成功证明了谷山-志村猜想，从而证明了费马大定理。可以说怀尔斯能证明费马大定理，是刚好生在一个合适的时代，并站在了巨人的肩膀上，从前人手中接过火炬。怀尔斯关于费马大定理的证明，就是这篇论文Modular elliptic curves and Fermat’s Last Theorem。该论文非常晦涩难懂，没多少人能看得懂，可以说能彻底看懂费马大定理证明的人，都是圈内大佬。论文中涉及的知识面很广，包括椭圆曲线、模形式、伽罗华表示论、代数数论、类域论、群概形等等，想要理解费马大定理就得先理解前面这些理论。不过虽然我们看不懂，但该证明还是非常具有收藏价值的，看不懂也能看，也能欣赏嘛。并且对于做算术几何的人来说，可以用这篇论文来指导自己的学习和研究。Peter Scholze当年不也一上来就看费尔马大定理的证明，虽然un ...

评审8年终获发表，数学天才望月新一证明abc猜想，全球只有十几个数学家读懂但争议未消

abc猜想，数学界悬而未决的重要猜想，它的证明过程经过8年的同行评审，终于要在期刊上发表了。论文作者是日本的天才数学家望月新一，他33岁起就在京都大学担任数学教授。这一次望月新一的证明，全篇超过600页，2012年就已发表，但足足经过了8年的同行评审才通过，期间开过多次研讨会——但依然有很多数学家无法理解。据说，这篇论文全球只有十几位数学家深入研究了证明过程。许多数学家根本无法指出证明过程是对是错，因为根本看不懂。4月3日，日本京都大学召开了新闻发布会，宣布望月新一证明了它。包括Nature等在内的权威科学传媒组织，也这一重要进展进行了报道。望月新一没有出席昨天的发布会，他的另外两位同事说，当他知道自己的论文被接收，终于松了一口气。多年来他从未在公众场合露面。但也不是没有争议，因为当初接收论文的期刊——日本的PRIMS，主编正是望月新一本人。如果他的证明是正确的，那么将彻底改变数论。同时也正因为如此，才有了学界长达8年的争论。什么是abc猜想？abc猜想，最初由法国数学家约瑟夫·奥斯特莱和大卫·马瑟，在1985年提出。并且一经提出，abc猜想就成为数论领域的重要猜想之一。只是和哥德巴赫 ...

望月新一与他天书般的论文，展现了纯数学与我们的距离

导语：一位日本数学家声称已经解决了数学领域最重要的问题之一。但是，几乎无人能懂他的证明，无从判断对错。2012年8月30日的早晨，望月新一悄悄地在自己的网站上发布了4篇论文，总计长达500多页，密密麻麻地布满了各种符号。它们是作者孤独工作了十多年后的成果，可能会在学术界引起爆炸性的影响。在文中，望月新一声称解决了abc猜想——一个27年来在数论领域一直悬而未决的问题，令所有其他数学家都束手无策。如果望月新一的证明是正确的，它将是本世纪最令人震撼的数学成果之一，或将彻底改变整数方程的研究。David Parkins不过，望月新一本人并未对自己的证明大做文章。他任职于日本京都大学数理解析研究所（RIMS），是一位令人尊敬的数学家。他没有向全世界的同行宣布自己的研究成果，只是将论文发布在网上，等待世界去发现。第一个注意到他的论文的可能是玉川安骑男（Akio Tamagawa）——望月新一在RIMS的同事。和其他研究人员一样，玉川安骑男知道望月新一多年来一直在潜心钻研abc猜想，并且已近成功。当天，玉川安骑男通过电子邮件把这个消息发给了他的合作者之一、诺丁汉大学数论理论家Ivan Fesenk ...

分析学大师Elias M. Stein的分析系列教材

分析学大师Elias M. Stein（曾是陶哲轩的老师），写了四本分析学系列教材，统称为普林斯顿分析学讲座（Princeton Lectures in Analysis）。他们分别是：I Fourier Analysis：An Introduction II Complex Analysis III Real Analysis: Measure Theory, Integration, and Hilbert Spaces IV Functional Analysis: Introduction to Further Topics in Analysis当时集齐这四本书花了我不少时间，似乎这四本书知名度不一，我下的第一本是复分析教材Complex Analysis。现在我将这些好东西拿出来分享给有需要的人。PS：如果需要中译版的，目前只能找到《实分析》和《复分析》两本，链接：伊莱亚斯 M. 斯坦恩（Elias M. Stein）《复分析》与《实分析》教材更新：作者不再提供附件下载。