这么多个搜索引擎就必应对弦圈最好了，谈谈弦圈过去的SEO经历

早在2024年4月4日弦圈上线之日，我就开始做弦圈的SEO优化，这期间免费付费手段都用过，效果也是起起伏伏。我并不是SEO方面的专家，这篇文章仅仅只是将我过去做SEO的经历说一下，以解释为什么最后我放弃SEO。

目前说到SEO优化，一般涉及的就是三大搜索引擎谷歌、百度、必应。其中谷歌全世界体量最大，百度国内体量最大，必应体量没前两者大。如果不考虑国外互联网，仅考虑国内的话，从趋势上看，谷歌对中文互联网不管不顾趋于平稳，百度则正在衰落，而必应则正在增长。在中文互联网中与SEO优化相关的内容，一般说的都是百度SEO或者谷歌SEO，然后大家一致的声音都是百度不行，谷歌行。

但网络上的信息往往都有滞后性，加上我是从零开始学习SEO相关知识，总之我持续花了好几个月专攻谷歌SEO，最后都没啥效果。为什么只做了几个月，因为我当时还没大学毕业但也快了。而网上那些所谓的SEO本来就慢，至少一年才有效果等等，在我看来都是p话，先不说我耗不起这样的时间，其次做了那么久那个曝光曲线还是差不多这样，根本没有上升的趋势，我不相信坚持到某天它会突然一飞冲天。

期间我试过自己按照网上的教程（国内外的教程都试过），写原创内容，做外链，最后都p用没有。然后我还试过去淘宝找代运营、整站优化，也试过直接买外链和买原创文章，最后通通都没用。这里对付费SEO提一嘴，少幻想便宜没好货，市面上那些SEO优化基本都是忽悠，真能做SEO的要么自己闷声发大财，要么价格贵得离谱。

至于为什么当时我专攻谷歌，放弃百度，因为事实摆在眼前谷歌收录得很快，我的网站刚上线提交Google Search Console，好像当天就收录了（其实具体多久记不清，但印象里就是快得离谱）。反观百度，简直是离谱到家，我做谷歌SEO这几个月它就只收录了一个首页，之后再也没动过。因此答案显而易见，收录都没收录，SEO优化个锤子🔨。后来事实证明放弃百度是对的，一年过去了百度都是动都没动，蜘蛛几乎就没爬过网站。

但是放弃百度对，不代表专攻谷歌对。 原本谷歌给我的流量就少得可怜，加上后面我的操作不当更是导致谷歌开始删除对弦圈的收录。在说我哪些操作不对前，先说个插曲，就是专攻几个月后见迟迟没效果，我也急了。一个人写原创文章累不说，还一点效果没有，于是我直接开始尝试搬运内容。因为我发现有些网站内容全是用爬虫自动搬的，一字不差，但是谷歌却给它流量，这让我极度不平衡，毕竟我的文章也被它搬了。更气人的是，这些搬运网站还挂了Google AdSense开始恰米了（打广告赚钱了），我自己原创的AdSense审核却不通过。

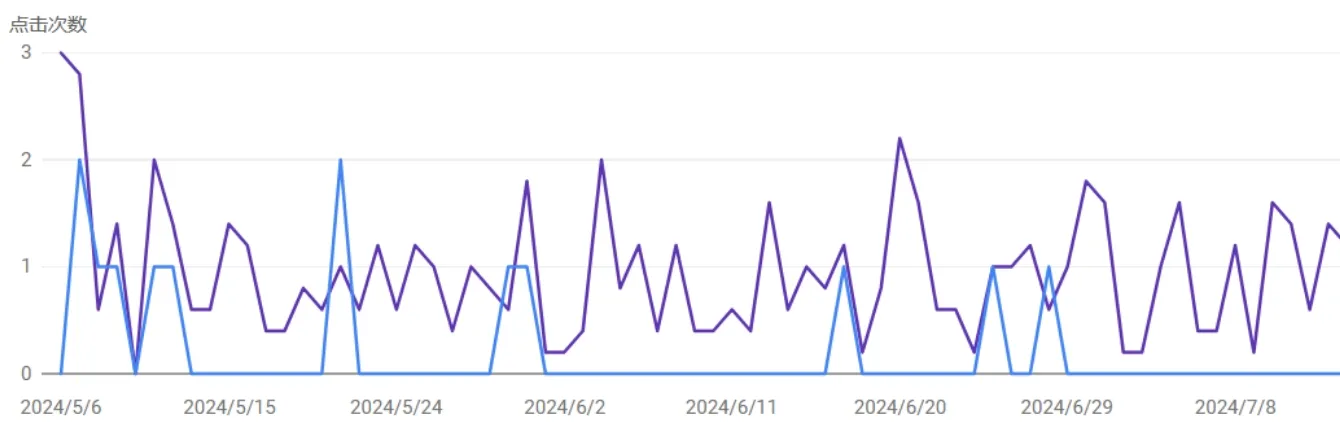
在我疯狂搬运这期间，谷歌的蜘蛛很活跃，爬弦圈爬得挺快，但是曝光量还是差不多，就是偶尔小升一下，又恢复正常，但也没有出现限流的情况。后面见搬运没啥效果，我就果断放弃了。后来事实也证明，搬运是错误的。我看到好几个靠搬运的网站，包括那个搬运我的，最后都被谷歌封杀了，网站直接死了。不过在我看来，这只是因为这些搬运网站的体量不够大，即搬运的量不够。有个网站叫啥头条（不是今日头条），内容全是搬运新闻的，到现在谷歌都给它推大量的流量。因为它的体量太大了，以至于直接攻克了搜索引擎，这就是所谓的内容农场污染搜索引擎的典型例子。

说回我的操作不当，先提一嘴，就是当时我用的网址还不是现在这个，而是manitori.xyz，现在这个xianquan.net是后来换的（弦圈更换新网址xianquan.net，原地址manitori.xyz保留）。我当时的主要问题就是对i18n的处理不当。我刚开始给弦圈直接设置了四种语言：中文、英文、法语、日文，结果最后发现自己翻译不过来，从而导致了大量垃圾页面的产生。我尝试过用AI来帮我翻译，但是都没能挽救这个问题。于是，后来我决定直接删掉法语跟日文，就留下如今的中文和英文。加上这个时间段，我还对网站进行过几次大改，导致URL变化，这些都最后导致产生了大量404页面。这也是问题的开始，记忆里从这时开始，谷歌似乎开始彻底认定弦圈是个垃圾网站，开始每天慢慢的删除对弦圈的收录。

为什么没有使用301跳转，因为页面太多，我不想一个个这样去设置301。这是由于当时设计上的一个缺陷，有很多页面的URL都是直接列举的方式来设置的，就数学我就列举了大量的分支，这也是间接导致很多垃圾页面的原因。总之，自那以后我还尝试过挽救弦圈的谷歌SEO，结果到如今快一年了，虽然更换域名后，情况有所好转，但谷歌还是不冷不淡的样子。

说到底，谷歌对于新站的容忍度是很低的，无论是谷歌还是百度都只有对高权重的网站很宽容。只要你经常变动你的网站，甚至有时候为了优化网站设计而不得不进行大改，这些都会损害谷歌SEO。但是必应却不同，它对新网站（至少对弦圈）的宽容度很高，从manitori.xyz开始到现在，弦圈不知道经历过多少次大变，必应对弦圈都是老样子。原本处处被我忽视的必应，如今却是每天如是的给弦圈推流，虽然给的流量不多，还跟谷歌和百度相比是相当不错了。

不知从什么时候开始百度也开始给我推流，但是当时我还只是收录一个首页，具体哪来的流量我也不知道，后台显示来源是m.baidu。而谷歌呢，就我专攻的那段时间偶尔施舍一两个点击（没错就是施舍），后面基本没咋给我流量。在这三个搜索引擎中，就必应对弦圈最好，推送的流量跟百度与谷歌加起来比，都不是一个量级。

三个月前我还在吐槽弦圈搜不到 弦圈在各大搜索引擎处于隐身状态，基本搜不到，但如今至少在必应是能搜到的。这里说的搜到不仅仅是收录，而是直接搜关键词能够看到网站。而百度与谷歌，即便现在也是搜不到。不过如今我也不是特别担心SEO的问题了，之前在 关于目前各大平台引流实践的总结：如今各大平台都在封锁流量，在这么一个垄断的大背景下，小平台只能在夹缝中生存...... 这篇文章中，我就提到自己已经放弃SEO，专攻社交媒体。

社媒当然也不好做，但是却比SEO更有希望。原因其实也很好理解，搜索引擎毕竟是很多年前就存在的东西了，位置早就被以前数不清的网站所占满。搜索引擎的流量肯定是先给他们的，剩下的给一些明星新网站，最后留给普通新网站的自然就不多了。社媒也是同理，但是社媒的体量要比搜索引擎小得多，所谓位置也早被占满，但是内卷程度远没有搜索引擎严重，故而能够分给普通用户的流量自然比搜索引擎多。