揭秘宇宙之谜：大爆炸的启示与无限终结的未来

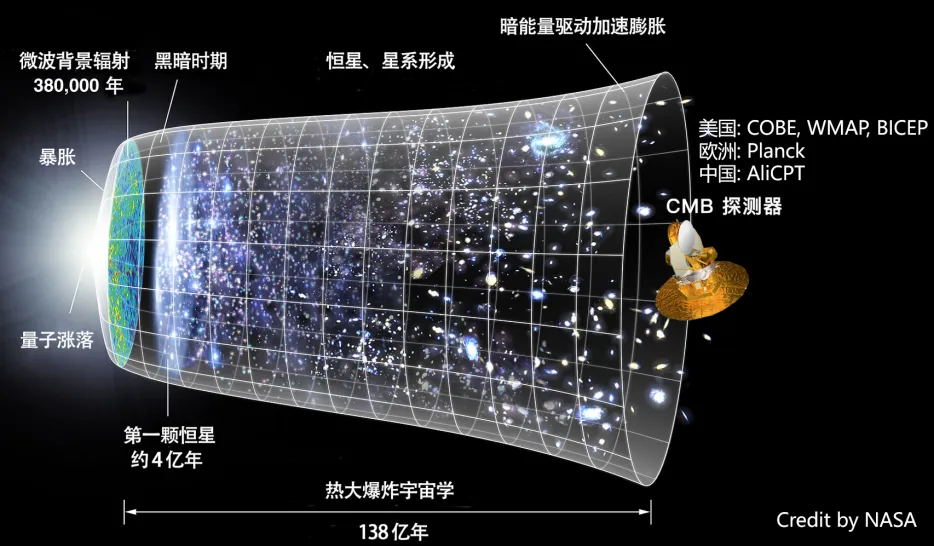
宇宙的形成始于最初的爆炸，这一观点不仅体现在爱因斯坦的理论中，还被视为宇宙学领域的核心指导原则。科学界普遍认为，在这场灾难性的爆炸之前，宇宙经历了特定的发展阶段。所谓的爆炸描述的是宇宙在极端的温度和密度条件下诞生的瞬间，大约发生在138亿年前，这一时期被称为“膨胀”。

在膨胀期间，宇宙以难以想象的速度迅速扩张，使其体积在极短的时间内翻倍，从不超过原子大小的状态迅速扩展到如今庞大的规模，包含了约3500亿个星系。这种极速扩张的过程如同魔法一般神奇。随着为这一过程提供能量的动力逐渐消散到太空，温度上升，物质粒子形成，我们现在称之为大爆炸的现象便出现了。

但是，关于引发膨胀的原因以及导致其结束的机制，仍然存在许多疑问。

关于膨胀持续的时间，我们无法给出确切的答案。我们对那个时期知之甚少，缺乏精确的数据。起初，一个微小而致密的物质球体开始膨胀，最终演变出原子、分子、恒星和星系，形成了我们今天所见的宇宙。然而，大爆炸之前发生了什么，以及那一刻之前的宇宙处于何种状态，这些问题仍然悬而未决。

在宇宙膨胀的过程中，宇宙的大小在不到一秒的时间里至少扩大了80倍。这个过程是由未知能量填充外太空真空所触发的瞬时膨胀，使得宇宙变得空旷而寒冷，为大爆炸创造了条件。

一些理论假设认为，膨胀并非突然停止，而是逐步、部分地结束。每一次膨胀过程的终止，都意味着一个新的宇宙的诞生。这些理论被称为“永久膨胀理论”，提出在这一过程中不断有新的宇宙形成，甚至可能是无限多个宇宙，超出了我们可以观察到的范围。

现代宇宙学正在积极探寻一些尚未完全解决的谜题的答案。宇宙膨胀的概念——即宇宙在大爆炸前极速扩张——为我们理解自身起源提供了新的视角。尽管如此，我们可能永远无法完全揭开在此之前所发生事件的神秘面纱。

多元宇宙理论为我们提供了一个观察无数宇宙的新视角，每个宇宙都有其独特的物理定律和常数。这些理论为解释为何我们的宇宙拥有如此理想的生命条件提供了可能的解释。如果存在着无数个具有不同物理定律组合的宇宙，那么必然存在一个最适合生命起源和维持的宇宙。

然而，值得注意的是，尽管宇宙膨胀的概念是现代宇宙学的基础，但关于多个宇宙的推测在科学上仍然是合理的假设。这一领域的研究仍在继续，科学家们孜孜不倦地寻找这些引人入胜的问题的答案。

我们的世界在不断变化，科学也不会停滞不前。现代宇宙学家正积极探索解释大爆炸之前过程的理论。其中一种理论是宇宙膨胀的概念，据此理论，在大爆炸前的时期，宇宙极其寒冷和空洞，其膨胀是由空间本身发出的能量引起的。

还有其他理论。其中之一是关于宇宙中存在额外维度的假设。根据这个假设，我们可以想象自己生活在广阔的多元宇宙中的一张纸上。在这个多元宇宙中，可能还有其他也在空间中移动的“纸片”或宇宙。这就提出了一个问题：当这些“薄片”相互碰撞时会发生什么。有一种理论认为，大爆炸是两个这样的“薄片”或膜碰撞的结果。

这些假设虽然颇具推测性，但实际上它们有着数学基础。此外，其中一些理论得到了实验的支持。例如，宇宙微波辐射是测试宇宙早期状态理论的关键工具。大爆炸后残留的辐射可以告诉我们很多有关那段时间发生的过程的信息。

我们知道我们所在的宇宙角落已经存在了138亿年。这正是光从我们肉眼可见的宇宙最遥远区域传播所需的时间。然而，我们的宇宙充满了许多奥秘和秘密。根据这些测量，我们可以推测宇宙超出了我们在“泡沫”中看到的范围。它延伸多远仍是个谜。我们还未能解答这个问题，但最新的科学发现和物理学测量表明宇宙可能是无限的。我们仍在努力寻找大爆炸之前发生了什么、我们可观测的宇宙有多大以及我们看到的部分之外还有什么等问题的答案。

然而，在思考万物的起源之后，我们经常忽视一个重要的问题：我们的宇宙将如何完成它的旅程？目前，最合理的假设是宇宙膨胀将持续无限期进行的观点。这一说法是基于一个令人惊讶的事实——宇宙的膨胀率随着时间的推移而增加。这种现象对我们来说是一个谜，因为直到此时，人们普遍认为引力作用于吸引力的方向，因此，从大爆炸那一刻开始的宇宙膨胀应该会减慢。我们还面临这样的问题：宇宙中是否有足够的物质来减缓其膨胀速度，使其停止膨胀并开始收缩。然而，表明宇宙膨胀正在加速的新发现表明，这个过程将持续下去，直到发生根本不同的事情。